Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.7 - Ex. 11

Suponha que a corda no Problema 10 começa a partir da posição inicial f ( x ) = 8 x ( L - x 2 ) / L 3 . Siga as instruções no Problema 10 para esse novo problema.

Passo 1

Letra a:

Temos a seguinte equação:

u ( x , t ) = ∑ n = 1 ∞ c n s i n n π x L c o s n π a t L

Daí, queremos achar o c n :

c n = 2 L ∫ 0 L f ( x ) s i n n π x L d x

Resolvendo, chegamos em:

c n = 512 3 c o s n π + ( 2 n - 1 ) π ( 2 n - 1 ) 4 π 4

Colocando na fórmula, chegamos em:

u ( x , t ) = 512 π 4 ∑ n = 1 ∞ 3 c o s n π + ( 2 n - 1 ) π ( 2 n - 1 ) 4 s i n ( 2 n - 1 ) π x 2 L c o s ( 2 n - 1 ) π a t 2 L

Passo 2

Na letra b:

Para L = 10   e   a = 1 , temos u ( x , t ) = 512 π 4 ∑ n = 1 ∞ 3 c o s n π + ( 2 n - 1 ) π ( 2 n - 1 ) 4 s i n ( 2 n - 1 ) π x 20 c o s ( 2 n - 1 ) π t 20

Segue o gráfico de u ( x , t ) por x para vários valores de t:

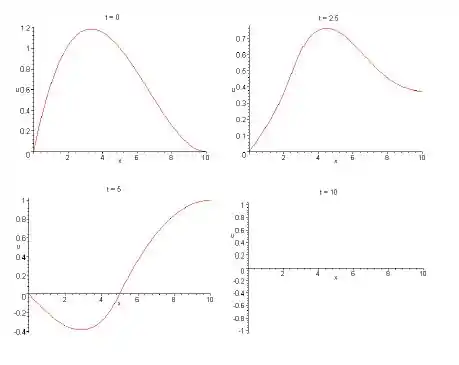
Passo 3

Letra c:

E agora, segue o gráfico de u ( x , t ) por t para vários valores de x :

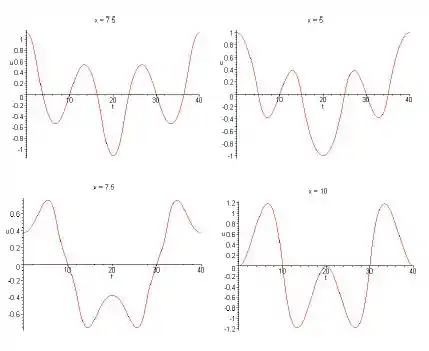
Passo 4

Letra d:

Para a animação, utilizar algum programa para gráficos animados.

Resposta

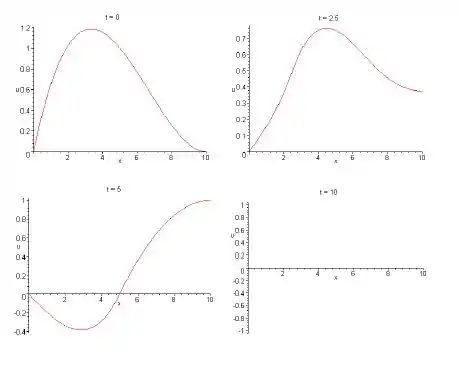
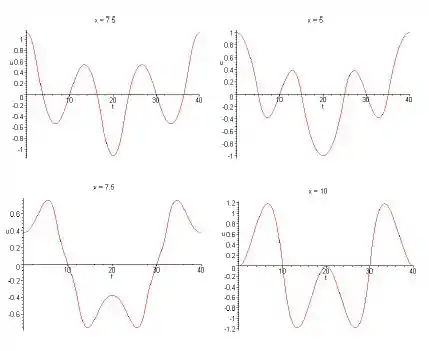
  1. u ( x , t ) = 512 π 4 ∑ n = 1 ∞ 3 c o s n π + ( 2 n - 1 ) π ( 2 n - 1 ) 4 s i n ( 2 n - 1 ) π x 2 L c o s ( 2 n - 1 ) π a t 2 L
  4. Para a animação, utilizar algum programa para gráficos animados.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se uma corda elástica tiver uma extremidade solta, a condição de contorno a ser satisfeita aí será u x = 0 . Encontre o deslocamento u(x, t) de uma corda elástica de comprimento L, fixa em x = 0 e sol
Faça o gráfico de ϕ ( x - a t ) para t = 0, 1/a, 2/a e t 0 / a se ϕ ( s ) = s e ns . Note que, para qualquer t ≠ 0 , o gráfico de y = ϕ ( x - a t ) é igual ao de y = ϕ ( x ) quando t = 0, só que deslo
Mostre que a equação de onda a 2 u x x = u t t pode ser reduzida à forma u x h = 0 pela mudança de variáveis ζ = x - a t ,η = x + a t Mostre que u(x, t) pode ser escrita como u ( x , t ) = ϕ ( x - a t
Considere uma corda elástica de comprimento L cujas extremidades são mantidas fixas. A corda écolocada em movimento a partir da sua posição de equilíbrio, com velocidade inicial ut(x, 0) = g(x). Em ca
Considere a equação de onda a 2 u x x = u t t em um meio unidimensional infinito, sujeita às condições iniciais u ( x , 0 ) = f ( x ) ,u t ( x , 0 ) = 0 ,- ∞x∞ . Usando a forma da solução obtida no Pr