Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 24
Enfocando conceitos
Sejam:
- Mostre que e
- Mostre que e não são inversas uma da outra provando que os gráficos dessas funções não são reflexões um do outro em relação à reta .
- As partes e se contradizem? Explique.
Passo 1
Fala povo, tudo ok? Ó só, tamos falando de funções compostas aqui. Pra começar, queremos:
Pô, pra achar isso, basta trocar todos os dentro de pela expressão inteira que define . Sendo assim:
E opa, essa ai é exatamente a definição de módulo de ! Veja que se eu inserir o resultado vai ser sempre . Inserindo , o resultado sempre será . Dados esses exemplos e sabendo que o módulo pode ser entendido como:
Como o enunciado disse que para , então realmente provamos que:
Agora pra outra igualdade, vamos manter a ideia, ok? Só que trocar a ordem de quem entra em quem:
E de novo, para , provamos que:
Passo 2
Show, agora vamos falar de inversas. Pra isso temos que isolar . Seja:
Para isolar tomamos a raiz quadrada no primeiro caso nos dois lados, e elevamos ao quadrado dos dois lados no segundo caso:
Pro primeiro caso, como , eliminamos o sinal de negativo. Além disso, da função original , podemos tirar que . Ou seja, reescrevemos:
E trocando e de lugar, achamos as inversas:
Agora bora comparar com as funções originais:
Pô galera, apesar de termos chegado bem perto, não é exatamente a inversa de visto que implica, obrigatoriamente em e não! A mesma lógica vale pra : a função não é sua inversa uma vez que não requer porém, ao contrário de .
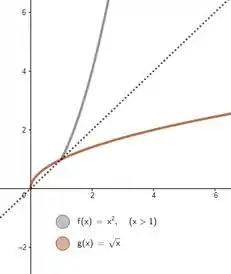
Pra fechar, vamos falar da letra . Pô galera, não tem porque os resultados de e se contradizerem uma vez que os procedimentos feitos (inversão de função e funções compostas) são completamente diferentes. Apesar do resultado da função composta ser exatamente o eixo de simetria das funções inversas, como existe a condição , faz sentido o resultado da letra ser verdade sem que sejam inversas uma da outra.
Resposta
Ei, a resposta está no passo a passo :)