Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.1 - Ex. 50
A equação de movimento de uma partícula é , em que está em metros e em segundos.
a) Encontre a velocidade e a aceleração como funções de .
b) Encontre a aceleração depois de segundo.
c) Trace o gráfico das funções posição, velocidade e aceleração na mesma tela.
Passo 1
O enunciado deu a função posição de uma partícula como função do tempo e pediu tanto a velocidade como a aceleração. Devemos lembrar da física que a velocidade é a derivada da posição e que a aceleração é a derivada da velocidade.
Passo 2
Para encontrar a velocidade como função de . Derivamos a equação da posição:
Agora, derivando a velocidade encontramos a aceleração :
Passo 3
Para encontramos a aceleração depois de segundo basta substituir na expressão da aceleração:
Passo 4
Para plotar o gráfico fazemos uma tabelinha:
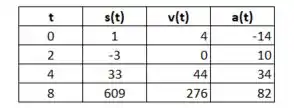
A posição é a curva em vermelho, a velocidade em azul e a aceleração em roxo:
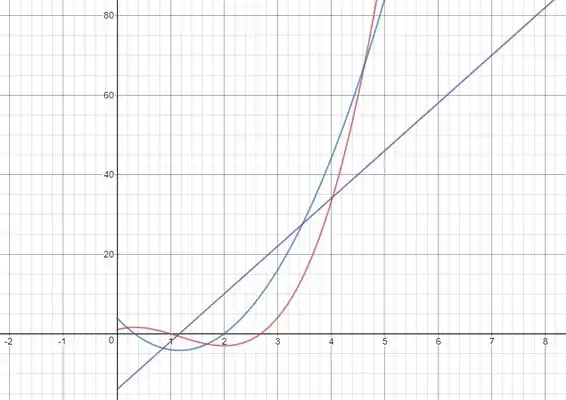
Resposta
a) e
b)
c) Esboço de gráficos.