A equação de movimento de um pêndulo sem amortecimento é d 2 θ d t + ω 2 s e n θ = 0 , onde ω 2 = g L . Faça x = θ ,y = d θ d t para obter o sistema d x d t = y ,d y d t = - ω 2 s e n x . a) Mostre que os pontos críticos são ± n π ,0 ,n = 0 , 1,2 , … . E que o sistema é quase linear na vizinhança de cada ponto crítico.b) Mostre que o ponto crítico 0,0 é um centro (estável) do sistema linear correspondente. Usando o Teorema 9.3.2, o que se pode dizer sobre o sistema não-linear? A situação é semelhante nos pontos críticos? ± 2 n π ,0 ,n = 1 ,2 ,3 … Qual a interpretação física desses pontos críticos?c) Mostre que o ponto crítico π ,0 é um ponto de sela (instável) do sistema linear correspondente. O que você pode concluir sobre o sistema não-linear? A situação é semelhante nos pontos críticos ± 2 n - 1 π ,0 ,n = 1 , 2,3 … . Qual a interpretação física desses pontos críticos? d) Escolha uma valor para ω 2 e faça o gráfico de algumas trajetórias do sistema não linear na vizinhança da origem. Você pode concluir mais alguma coisa sobre a natureza do ponto crítico 0,0 para o sistema não linear?e) Usando o valor de ω 2 do item (d), desenhe um retrato de fase para o pêndulo. Compare seu gráfico com o da Fig 9.3.5 para o pêndulo com amortecimento.

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 19

A equação de movimento de um pêndulo sem amortecimento é , onde Faça para obter o sistema

a) Mostre que os pontos críticos são E que o sistema é quase linear na vizinhança de cada ponto crítico.

b) Mostre que o ponto crítico é um centro (estável) do sistema linear correspondente. Usando o Teorema 9.3.2, o que se pode dizer sobre o sistema não-linear? A situação é semelhante nos pontos críticos? Qual a interpretação física desses pontos críticos?

c) Mostre que o ponto crítico é um ponto de sela (instável) do sistema linear correspondente. O que você pode concluir sobre o sistema não-linear? A situação é semelhante nos pontos críticos . Qual a interpretação física desses pontos críticos?

d) Escolha uma valor para e faça o gráfico de algumas trajetórias do sistema não linear na vizinhança da origem. Você pode concluir mais alguma coisa sobre a natureza do ponto crítico para o sistema não linear?

e) Usando o valor de do item (d), desenhe um retrato de fase para o pêndulo. Compare seu gráfico com o da Fig 9.3.5 para o pêndulo com amortecimento.

Passo 1

a) A solução do sistema de equações

consiste dos pontos A função são analíticas em todo plano. Isso nos da que o sistema é quase linear próximo aos pontos críticos.

Passo 2

b) A matriz jacobianda do campo de vetores nos é dado por

Na origem, o coeficiente matricial do sistema linearizado é

com autovalores complexos Logoa origem é um centro. Como os autovalores são complecos, o teorema 9.3.2 não nos da definisões conclusivas sobre o ponto crítico do sistema não linear.

Fisicamente, o ponto critico corresponde ao estado Isso é, a configuração de repouso do pêndulo.

Passo 3

c) No ponto crítico , o coeficiente matricial do sistema linearizado é

com autovalores Os autovalores são reais e de sinais opostos, logo sabemos que é um ponto de sela. O teorema 9.3.2 afirma que o ponto crítico para o sistema não-linear é uma sela, que é instável. Fisicamente, o ponto critico corresponde ao estado Isso é, a configuração de repouso do pêndulo na posição vertical.

Passo 4

d) Façamos Seguindo o esboço das fases das curvas próximas a origem

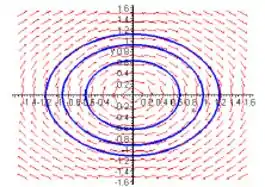
Isso nos mostra que a origem é realmente um centro.

Passo 5

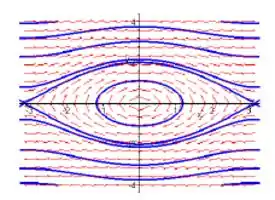
Deve ser dito que que a fase representada segue um padrão.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os pontos críticos.

Determine o comportamento limite de x e y quando t → ∞ e interprete os resultados em termos das populações das duas espécies..

Esboce as trajetórias em uma vizinhança de cada ponto crítico. Calcule e faça o gráfico de um número suficiente de trajetórias do sistema dado de modo a mostrar, claramente, o comportamento das soluçõ

Desenhe um campo de direções e descreva como as soluções parecem se comportar.