(a) O que a equação representa como uma curva em ?
(b) O que ela representa como uma superfície em ?
(c) O que a equação representa?
Passo 1
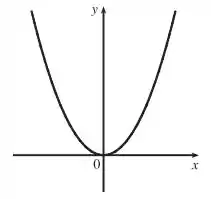
(a) E aí, galera? Em , a equação representa uma parábola, certo?
Passo 2
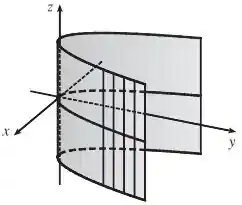
(b) Já em , a mesma equação representa um cilindro parabólico. Mas o que é isso? É como se houvesse infinitas parábola, uma colada na outra, ao longo do eixo , formando tipo um túnel de parábolas, um cilindro de parábolas, por isso tem esse nome.
Passo 3
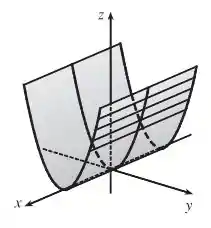
(c) O formato da equação de nos lembra o item anterior, ou seja, a equação também representa um cilindro parabólico. Mas agora, no lugar de , temos . Então é como se agora as parábolas formassem um cilindro ao longo do eixo , não do eixo (é a variável que não aparece na equação que determina isso). Mais formalmente, a gente diz que a geratriz do cilindro é paralela ao eixo , tá beleza?
Resposta
(a) Parábola
(b) Cilindro parabólico com geratriz paralela ao eixo
(c) Cilindro parabólico com geratriz paralela ao eixo