Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 9.2 - Ex. 1b
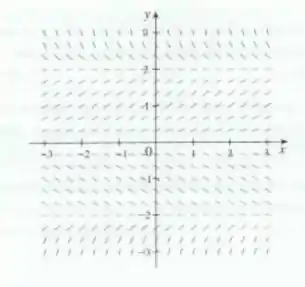
É mostrado um campo de direções para a equação diferencial:
Ache todas as soluções de equilíbrio.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos essa equaçãozinha aii e depois dar o resultado. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser analisar qual a direção e qual o sentido que as nossas linhas do gráfico estão indo. Como já sabemos, o nosso gráfico vai ter uma linha cortando em cada um daqueles valores dados nas condições, já que ele deu para y(0).
Olhado isso, agora vamos observar como as linhas se comportam antes e depois desses pontos e traçar o as nossas curvas.
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
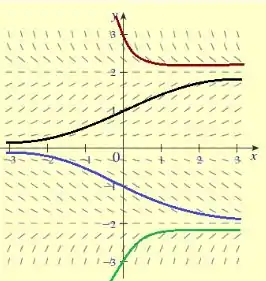
Nós podemos ver que os vetores nunca se encostam nas linhas y=-2, y=0 e y=2. Com isso, podemos concluir que essas são as soluções de equilíbrio.
Resposta
Nós podemos ver que os vetores nunca se encostam nas linhas y=-2, y=0 e y=2. Com isso, podemos concluir que essas são as soluções de equilíbrio.