Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 46

Equações de Laplace. Seja w = f u + g v , onde u = x + i y , v = x - i y e i = - 1 . Mostre que w satisfaz a equação de Laplace w x x + w y y = 0 se todas as funções necessárias forem diferenciáveis.

Passo 1

Oi pessoal, tudo bem com vocês? Vamos lá!

Relembrando que para uma função f x ,   y , a equação de Laplace é:

∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = 0

Ou:

f x x + f y y = 0

Para satisfazer   w x x + w y y = 0 , podemos dizer que:

  w x x + w y y = ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 = 0

Pelo nosso diagrama de árvore:

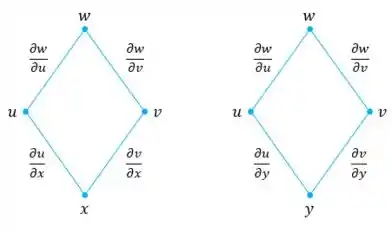
Conseguimos definir nossas derivadas de segunda ordem pela Regra da Cadeia:

Então:

∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 = ∂ 2 w ∂ u 2 ∂ 2 u ∂ x 2 + ∂ 2 w ∂ v 2 ∂ 2 v ∂ x 2 + ∂ 2 w ∂ u 2 ∂ 2 u ∂ y 2 + ∂ 2 w ∂ v 2 ∂ 2 v ∂ y 2

Passo 2

Sendo assim, para u = x + i y . As derivadas de primeira e segunda ordem são:

∂ u ∂ x = 1 → ∂ 2 u ∂ x 2 = 0

∂ u ∂ y = i → ∂ 2 u ∂ y 2 = 0  

E para v = x - i y :

∂ v ∂ x = 1 → ∂ 2 v ∂ x 2 = 0

∂ v ∂ y = - i → ∂ 2 v ∂ y 2 = 0  

Passo 3

Substituindo os valores encontrados na equação do Passo 1:

∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 = ∂ 2 w ∂ u 2 ∂ 2 u ∂ x 2 + ∂ 2 w ∂ v 2 ∂ 2 v ∂ x 2 + ∂ 2 w ∂ u 2 ∂ 2 u ∂ y 2 + ∂ 2 w ∂ v 2 ∂ 2 v ∂ y 2

∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 = ∂ 2 w ∂ u 2 ∙ 0 + ∂ 2 w ∂ v 2 ∙ 0 + ∂ 2 w ∂ u 2 ∙ 0 + ∂ 2 w ∂ v 2 ∙ 0

∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 = 0

Então podemos dizer que w satisfaz a equação de Laplace:

w x x + w y y = 0

Prontinho pessoal, te espero em breve para fazermos mais exercícios juntos!

Resposta

Respostas nos Passos.

Exercícios de Livros Relacionados

Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada. ∂ w ∂ x e ∂ w ∂ y para w = g u ,v , u = h x ,y , v = k x ,y
Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada. d z d t para z = f u ,v ,w , u = g t , v = h t , w = k t
Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada. ∂ z ∂ t e ∂ z ∂ s para z = f x ,y , x = g t ,s , y = h t ,s
Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada. ∂ w ∂ u e ∂ w ∂ v para w = h x ,y ,z , x = f u ,v , y = g u ,v , z = k u ,v
Nos Exercícios 13-24, desenhe um diagrama de árvore e escreva uma fórmula da regra da cadeia para cada derivada. ∂ w ∂ x e ∂ w ∂ y para w = f r ,s ,t , r = g x ,y , s = h x ,y , t = k x ,y