As equações paramétricas da trajetória de um cometa são dadas em função do tempo por

e ,,

Onde e são medidas expressas em unidades astronômicas .

Calcule a curvatura da órbita em um ponto qualquer da mesma.

Encontre os pontos de máximo e mínimo para a curvatura.

Sugestão: O máximo (mínimo) da curvatura é o mínimo (máximo) do raio de curvatura .

Então, a partir da fórmula da curvatura da órbita:

Vemos que o método de derivação a ser usado é a regra do quociente dada por:

Assim, derivando-a, temos:

Ou seja:

Juntando os termos semelhante:

Enfim, igualando a derivada a zero:

Multiplicando ambos os lados pelo denominador, teremos:

Se isolarmos as funções trigonométricas:

Para que o resultado seja nulo, uma das funções trigonométricas deve ser zero. Assim, se:

E se:

Analisando os intervalos entre os pontos, conseguimos saber o comportamento da função em cada trecho. Para tanto, precisamos saber se o valor da primeira derivada é maior ou menor que zero em cada trecho. Se ela for positiva, a função é crescente; se ela for negativa, a função é decrescente.

Ainda, o ponto em que a função deixa de ser decrescente e passa a ser crescente é um ponto de mínimo valor; caso contrário, o ponto é de máximo valor.

A seguir está uma análise do valor da derivada em cada trecho entre os pontos:

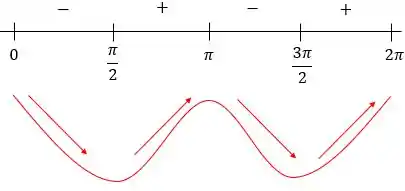
Visto que os pontos e são os maiores em suas proximidades, eles são pontos de máximo valor.

O ponto também é de máximo valor, pelo fato de que a função passar de ser crescente para decrescente.

Já nos pontos e , a função passa de decrescente para crescente e, por isso, são pontos de mínimo valor.

Logo, concluímos que os pontos de máximo da curvatura são:

E:

Enquanto os pontos de mínimo são:

E: