Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.14 - Ex. 19b
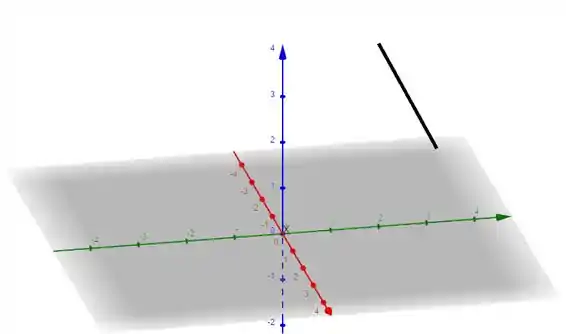
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.
b) ,
Passo 1
A curva que ele nos deu foi a seguinte:
Assim,
Opa, mas isso representa uma reta no . Fazendo um esboço:
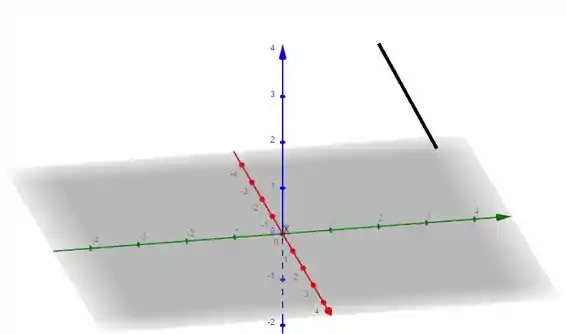
Onde o sentido positivo é para baixo ao longo da reta.
Passo 2
Para finalizar, ele nos pede para encontrarmos a parametrização com a orientação no sentido contrário.
Repare que estamos com valores de . Então para pegarmos o sentido contrário, vamos trocar por . Assim,
Portanto,
,
Resposta
,
Exercícios de Livros Relacionados
Faça um esboço das curvas definidas pelas seguintes funções vetoriais:
Faça um esboço das curvas definidas pelas seguintes funções vetoriais:
Dê uma parametrização para cada uma das curvas.
Dê uma parametrização para cada uma das curvas.
Uma haste, presa na origem do plano x y , ocupa a posição da reta x = t y . A haste intercepta a reta y = 4 no ponto S e a elipse 4 x 2 + y - 2 2 = 4 no ponto Q . Quando t varia, o vértice P do triâng