Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.5 - Ex. 18c

Esboçar a região de integração e calcular as integrais

Passo 1

Lembra que na integral tripla o é a mesma coisa que , então sabemos que as integrais triplas podem ser calculadas de forma análoga às integrais duplas, por meio de integrações sucessivas.

Para calcular as integrais duplas precisávamos ter noção da região de integração, aqui em integrais triplas vamos precisar da mesma noção e isso é justamente iterar a nossa integral tripla.

Passo 2

Na nossa integral vemos que a ordem de integração é dz, depois dy e por fim dx, logo, a partir dessa informação podemos tirar os nossos limites para cada variável

Portanto,

Isso nos dá a seguinte região T :

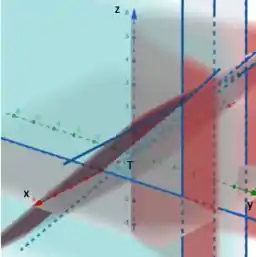
Que é a região abaixo do plano e acima de e a parte de fora do cilindro cuja a diretriz é até o plano

Passo 3

Agora, vamos resolver nossa integral

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a integral tripla para determinar o volume do sólido dado.O sólido limitado pelo cilindro x 2 + y 2 = 9 e pelos planos y + z = 5 e x = 1 .

Calcule a integral tripla ∭ E x d V Onde E é limitado pelo parabolóide x = 4 y 2 + 4 z 2 e pelo plano x = 4

Esboçar a região de integração e calcular as integrais:g) ∫ 0 2 ∫ 0 1 2 4 - x 2 ∫ 0 x 2 + 4 y 2 d z d y d x

Esboçar a região de integração e calcular as integrais:h) ∫ - 3 3 ∫ - 9 - y 2 9 - y 2 ∫ 4 x 2 + 4 y 2 - 9 3 x 2 + 3 y 2 d z d x d y

Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T d V Onde T é a região delimitada por x=y 2 ,y = x 2 ,z = 2 y ,z = - 2 y .