Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 18
Use a integral tripla para determinar o volume do sólido dado.
O sólido limitado pelo cilindro e pelos planos e .
Passo 1
Olá, desbravador dos números! Vamos explorar e solucionar essa questão de cálculo juntos. Partiu!
Para solucionar essa questão vamos usar a integral tripla para determinar o volume do sólido limitado pelo cilindro e pelos planos e .
Temos que o sólido descrito pelo enunciado é:
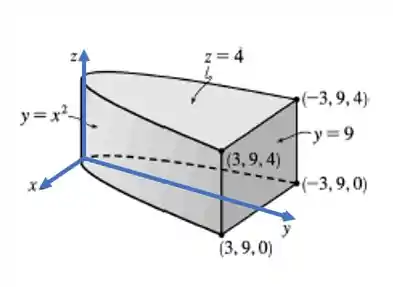
Para calcular o volume desse sólido, usamos a integral tripla:
Pelo esboço do sólido temos as seguintes condições:
- O cilindro indica que varia de a (pois varia de a ).
- O plano estabelece um limite fixo para .
Passo 2
Portanto, os limites de integração são determinados da seguinte forma:
- Para , varia de a pois o cilindro .
- Para um dado , varia de a , garantindo que permaneça dentro do cilindro.
- varia de a , limitado pelo plano .
Com esses limites de integração definidos, a integral que representa o volume do sólido é:
Passo 3
Agora, podemos resolver a integral de dentro para fora. Integrando em relação a :
Integrando em relação a :
Integrando em relação a :
Calculando esta integral:
Calculando os limites: