Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.5 - Ex. 18g

Esboçar a região de integração e calcular as integrais:

g) ∫ 0 2 ∫ 0 1 2 4 - x 2 ∫ 0 x 2 + 4 y 2 d z d y d x

Passo 1

Bora continuar!

Nós vamos começar resolvendo as integrais de dentro para fora, ok?

Então vamos começar com a integral:

∫ 0 x 2 + 4 y 2 d z = z   | x 2 + 4 y 2 0

Aplicando o intervalo:

= x 2 + 4 y 2 - 0 = x 2 + 4 y 2

Este resultado nós colocamos dentro da segunda integral:

∫ 0 1 2 4 - x 2 ( x 2 + 4 y 2 ) d y

Agora é só resolver:

= ∫ 0 1 2 4 - x 2 x 2 d y + ∫ 0 1 2 4 - x 2 4 y 2 d y

= x 2 y + 4 y 3 3 1 2 4 - x 2 0

E aplicamos este novo intervalo:

= x 2 1 2 4 - x 2 - 0 + 4 3 1 2 4 - x 2 3 - 0 3

= x 2 2 4 - x 2 + 4 3 4 - x 2 3 2 8

= x 2 2 4 - x 2 + 4 - x 2 3 2 6

Passo 2

Agora colocamos este resultado dentro da última integral:

∫ 0 2 x 2 2 4 - x 2 + 4 - x 2 3 2 6 d x

Para resolver precisamos reorganizar, ok?

= 1 2 ∫ 0 2 x 2 4 - x 2 d x + 1 6 ∫ 0 2 4 - x 2 3 2 d x

Vamos começar resolvendo a primeira integral:

∫ 0 2 x 2 4 - x 2 d x

Se chamarmos:

x = 2 s e n   ( u )

d x = 2 cos ⁡ ( u ) d u

Os intervalos de integração agora serão:

s e n   u = 0 → u = 0

s e n   u = 1 → u = π 2

Então:

= ∫ 0 π 2 2 s e n   u 2 4 - 2 s e n   u 2 ( 2 cos ⁡ u d u ) = 8 ∫ 0 π 2 s e n 2   ( u ) cos ⁡ u 4 - 4 s e n 2   ( u ) d u

= 8 ∫ 0 π 2 s e n 2   ( u ) cos ⁡ u 4 ( 1 - s e n 2   u ) d u

Lembrando da identidade:

cos 2 ⁡ ( u ) = 1 - s e n 2   u

Então:

= 8 ∫ 0 π 2 s e n 2   ( u ) cos ⁡ u 4 cos 2 ⁡ ( u ) d u = 16 ∫ 0 π 2 s e n 2   ( u ) cos 2 ⁡ u d u

Usando outra identidade:

s e n 2   ( u ) cos 2 ⁡ u = 1 - cos ⁡ ( 4 u ) 8

Substituímos:

= 16 ∫ 0 π 2 1 - cos ⁡ ( 4 u ) 8 d u

= 2 ∫ 0 π 2 d u - ∫ 0 π 2 cos ⁡ 4 u d u

= 2 u + ∫ 0 π 2 cos ⁡ 4 u d u

Chamando:

w = 4 u

d w = 4 d u → d w 4 = d u

Nossa integral será:

= 2 u + ∫ 0 π 2 cos ⁡ w d w 4 = 2 u + 1 4 ∫ 0 π 2 cos ⁡ w d w

= 2 u + s e n   ( w ) 4 π 2 0

Substituindo u:

= 2 u + s e n   ( 2 u ) 4 π 2 0

Aplicando o intervalo:

= 2 π 2 - 0 + 1 4 s e n   π - s e n   0

= 2 π 2 + 1 2 0 - 0

Então:

1 2 ∫ 0 2 x 2 4 - x 2 d x = π 2

Passo 3

Agora vamos resolver a próxima:

1 6 ∫ 0 2 4 - x 2 3 2 d x

Vamos resolver por partes:

u = 4 - x 2 3 2

d u = 3 2 4 - x 2 1 2 - 2 x d x = - 3 x 4 - x 2 1 2 d x

d v = d x

v = x

Então:

= 1 6 x 4 - x 2 3 2 - ∫ 0 2 - 3 x 2 4 - x 2 1 2 d x

= 1 6 x 4 - x 2 3 2 + 3 ∫ 0 2 x 2 4 - x 2 1 2 d x

Já sabemos que:

∫ 0 2 x 2 4 - x 2 1 2 d x = π

Então:

= 1 6 x 4 - x 2 3 2 + 3 π 2 0

= 1 6 2 4 - 2 2 3 2 + 3 π

= 1 6 3 π = π 2

Então o resultado será:

π 2 + π 2 = π

Desenhando, nossa superfície ficará mais ou menos assim:

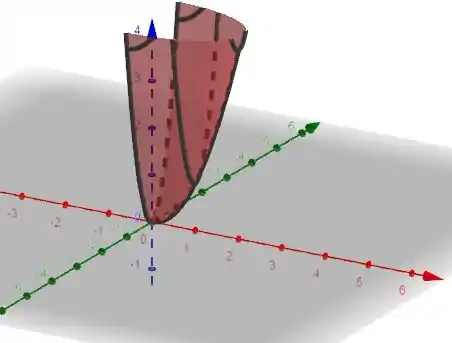
E acabamos !

Resposta

∫ 0 2 ∫ 0 1 2 4 - x 2 ∫ 0 x 2 + 4 y 2 d z d y d x = π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboçar a região de integração e calcular as integrais ∫ 0 4 ∫ y 2 ∫ 0 y y d z d x d y
Esboçar a região de integração e calcular as integrais ∫ 1 2 ∫ x 2 x ∫ 0 x + y z d z d y d x
Esboçar a região de integração e calcular as integrais ∫ 1 2 ∫ 0 x 2 ∫ 0 1 x x 2 y 2 z d z d y d x
Calcule
Calcule