Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 3a
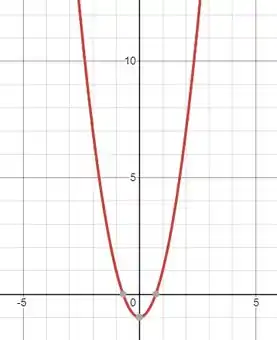
Esboçar a trajetória de uma partícula , sabendo que seu movimento é descrito por:
Passo 1
Pessoal, vamos abrir essa função de movimento nas componentes e :
Como , podemos subsituir esse valor na equação de . Assim,
Caímos numa equação conhecida aqui! Temos uma parábola! Logo,
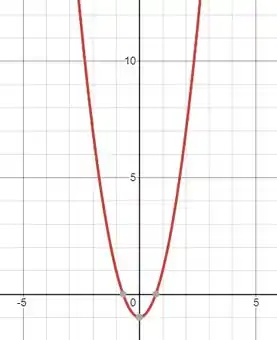
Resposta
A trajetória é igual a:
Exercícios de Livros Relacionados
Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. x = e t ,y = t e t ,z = t e t 2 ; ( 1,0 , 0 )
Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. x = t 2 + 3 ,y = ln ( t 2 + 3 ) ,z = t ; ( 2 , ln 4 , 1 )
Encontre uma equação para a reta tangente à curva de intersecção dos cilindros x 2 + y 2 = 25 e y 2 + z 2 = 20 no ponto ( 3,4 , 2 ) .
Mostre que o vetor tangente a uma curva definida por uma função vetorial r(t) aponta no mesmo sentido da curva com t aumentando. [Dica: Consulte a Figura 1 e considere os casos h0 e h0 separadamente.]
Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de t