Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.2 - Ex. 14
Esboce um campo de direção para a equação diferencial. Em seguida, use-o para esboçar uma curva de solução que passa por um determinado ponto.
Passo 1
Falaaa moçadinhaaa bora laáaa??
Devemos encontrar o campo de direção para a função fornecida mostrada abaixo:
O campo de direção para esta função é :
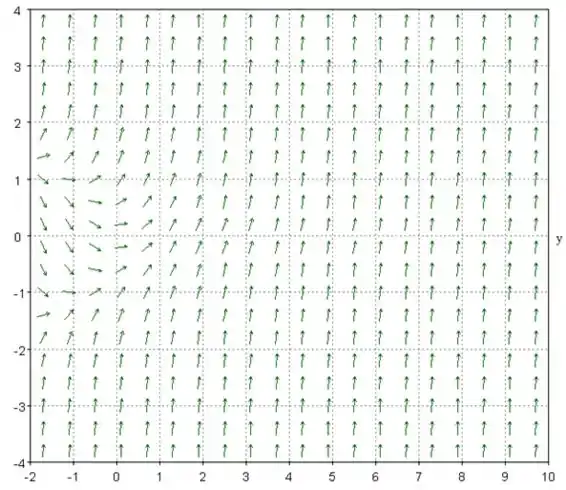
Passo 2
Agora iremos esboçar uma curva de solução que passa em (0, 0)
Resposta
Vide a explicação.
Exercícios de Livros Relacionados
6. Calcular ∫ C 2 x z + y 2 d x + 2 x y d y + x 2 d z , onde C é a intersecção das superfícieis z = x 2 + y 2 e x + y = 2 do ponto A(2,0,4) a B(0,2,4).
10. Uma partícula de massa m move-se no plano xy sob influência da força gravitacional F → = - m gj → . Se a partícula move-se de (0,0) a (-2,1) ao longo de um caminho C, mostrar que o trabalho realiz
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(c) segmento de reta que une o ponto A(0,1,0) ao ponto B(1,0, 3 )
12. Determinar o trabalho realizado pela força f → = y z e x z ,e x z , x y e x z + 1 para deslocar uma partícula ao longo da curva y=2/x do ponto A(-1,-2,0) ao ponto B(-2,-1,0). Esse trabalho é maior
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(d) intersecção das superfícies z = x 2 + y 2 , x=2, do ponto A(2,0,2) a B(2,4,2 5 )