As linhas de escoamento (ou linhas de corrente) de um campo vetorial são as trajetórias seguidas por uma partícula cujo campo de velocidade é um campo vetorial dado. Assim, os vetores do campo vetorial são tangentes a suas linhas de escoamento.
- Esboce o campo vetorial e algumas linhas de escoamento. Qual é o formato que essas linhas de escoamento parecem ter?
- Se as equações paramétricas das linhas de escoamento são que equações diferenciais essas funções satisfazem? Deduza que .
- Se uma partícula está na origem no instante inicial e o campo de velocidade é dado por , determine uma equação para a trajetória percorrida por ela.
Passo 1
E aiiii meu povo, beleza? Vamos começar.
Vamos com muita calma e atenção, beleza!! Porque essa questão tem bastante informação.
No item (a) precisamos esboçar o campo vetorial e algumas linhas de escoamento para . E também falar qual o formato que essas linhas de escoamento parecem ter.
No item (b), precisamos determinar que equações diferenciais as equações paramétricas das linhas de escoamento são satisfazem? Deduzir que .
Por fim, no item (c) precisamos determinar uma equação para a trajetória de uma partícula que no instante inicial está na origem e o campo é dado por .
Bastante informação né! Mas vamos montar uma estratégia para cada uma delas, certo?
Para o item (a) vamos precisar avaliar cada quadrante, e assumir valores dentro do quadrante e entender qual a direção do vetor. Sabendo a direção do campo de vetores, sabemos a direção da linha de escoamento, e a partir da linha de escoamento podemos estimar uma equação.
Já no item (b), precisamos deduzir que . Para fazer isso, vamos partir da seguinte analise:
Olhando pra , vemos que as seguintes equações devem ser satisfeitas:
Veja que agora podemos provar , tirando a razão entre e .
Por fim, no item (c) devemos resolver a equação diferencial do item (b):
Aplique o ponto da origem , para encontra a constante.
Galerinha, faça com bastante calma esse exercício beleza?! Para entender cada etapa!
Vamos nessa!!!
Passo 2
Começando pelo item (a).
Temos a seguinte função do campo vetorial:
Observe que a componente desse vetor, é sempre fixa e vale .
Antes de tudo lembre quem é cada quadrante:
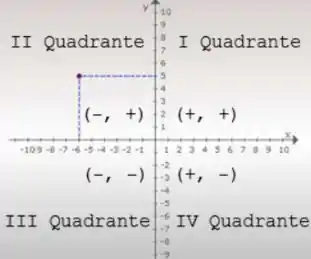
Para o primeiro quadrante, vamos pegar os pontos:
Aplicando em , temos:
Observe que o vetor está direcionado para o eixo positivo de y e para o eixo positivo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Para o segundo quadrante, vamos pegar os pontos:
Aplicando em , temos:
Agora o vetor está direcionado para o eixo negativo de y e para o eixo positivo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Para o terceiro quadrante, vamos pegar os pontos:
Aplicando em , temos:
Perceba, que o vetor está direcionado para o eixo negativo de y e para o eixo positivo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Por fim, o quarto quadrante, vamos pegar os pontos:
Aplicando em , temos:
Perceba, que o vetor está direcionado para o eixo positivo de y e para o eixo positivo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Passo 3
Vimos no passo 2 o comportamento do vetor em cada quadrante.
Com base nisso podemos estimar que o campo vetorial vai ter o seguinte padrão:
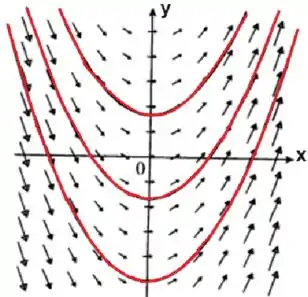
Bom, observe as linhas em vermelhos. Essas são as linhas de escoamento, e repare que elas seguem o sentido dos vetores.
Analisando bem essas linhas, podemos dizer que elas têm formato de parábolas.
Passo 4
Para o item (b) nosso objetivo principal é deduzir:
Vamos avaliar:
Do enunciado sabemos que as equações paramétricas das linhas de escoamento são . Que equações diferenciais essas funções satisfazem?
Vemos que as seguintes equações devem ser satisfeitas:
Porque isso? Porque a velocidade de uma partícula é dada pela derivada de sua posição em relação ao tempo:
Onde,
Logo:
Para que a trajetória siga o campo vetorial, a velocidade da partícula deve ser igual à força (ou velocidade) dada pelo campo vetorial em cada ponto. Portanto:
A partir disso, conclui-se que:
Perceba que se fizermos a razão entre essas duas equações, vamos conseguir deduzir. Veja só:
Simplificando temos que:
Passo 5
Por fim, vamos resolver o item (c).
Pra determinar uma equação para a trajetória percorrida pela partícula, vamos resolver a equação diferencial:
Vamos começar isolando .
Integrando, temos:
Pra determinar a constante , basta usar o fato de que a partícula estava na origem no instante inicial, ou seja, a linha de escoamento passa por :
Então, chegamos à equação:
Resposta
(a)
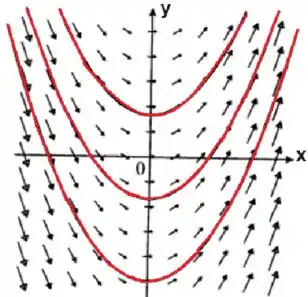
(b)
(c)