Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 20
Seja , onde e . Use um SCA para traçar esse campo vetorial em vários domínios, até conseguir visualizar o que ocorre. Descreva a aparência do desenho e explique-o, determinando os pontos onde .
Passo 1
E aiii galera, beleza?
Temos o seguinte campo:
, onde e .
Com base nisso, devemos usar um SCA para traçar o campo vetorial em vários domínios, até compreender oque ocorre. Assim, descrever e explicar a aparência do desenho, determinado onde
Muita calma agora?
Vamos lembrar o que quer dizer SCA: significa um Sistema de Computação Algébrica (SCA)
Sugiro utilizar o software Mathematica, mas pode usar algum outro de sua preferência.
Para entrar no software com a função do campo, o primeiro passo é reescrever o campo em função de e . Para isso basta você substituir pelo módulo do vetor e substituir .
Com essa equação você conseguirá plotar o campo vetorial.
Já para determinar o valor que , é só igualar a zero o campo vetorial. Assim:
Onde,
Para saber onde o campo vai ser zero, basta analisarmos onde o termo que está multiplicando a componente vai ser zero.
Agora ficou moleza em pessoal!!! Vamos nessa!
Passo 2
Vamos primeiro escrever nosso campo em função de e .
Sabemos que e .
Vamos obter , fazendo o módulo temos:
Substituindo em , temos:
Assim, temos o seguinte campo:
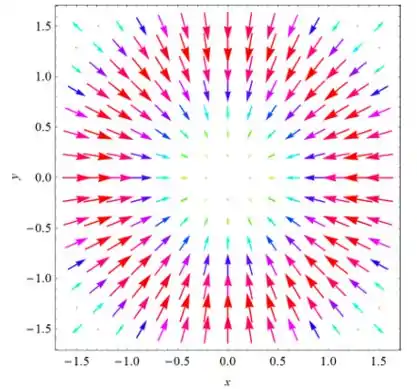
Agora vamos plotar esse campo. Usando o comando VectorPlot no software Mathematica, obtemos:
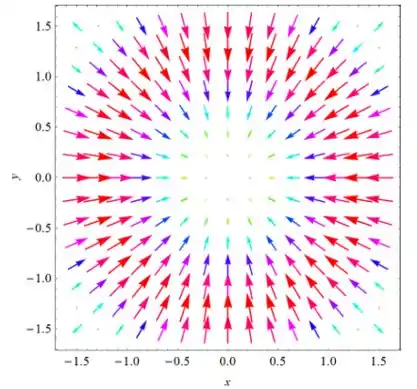
Observe que temos umas distribuições circulares dos vetores, e até o círculo de raio os vetores apontam para o centro. Observe também, que no centro onde o raio é igual a e na região onde o raio é igual a o campo é nulo.
Passo 3
Agora vamos analisar a condição para que .
Onde,
Para saber onde o campo vai ser zero, basta analisarmos onde o termo que está multiplicando a componente vai ser zero. Logo,
Ou seja, como visto na figura, os vetores em torno da origem até a circunferência têm magnitude que se aproximam de .
Resposta
