Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 1
Esboce o campo vetorial desenhando um diagrama como o da figura ou da Figura
Passo 1
Falaaaaaaiiii, vamos lá resolver essa questão?! Simbora! Nosso enunciado deu esse campo vetorial:
Só pra gente ficar com o conceito na cachola, o campo vetorial nos diz que, de determinado ponto , irá sair um vetor cuja direção, sentido e módulo dependem das coordenadas desse ponto!
Então pra esboçar um campo vetorial tudo que a gente precisa fazer é testar alguns pontos e ir desenhando os vetores, até achar o padrão e poder aplicar isso pra todos os pontos.
Passo 2
Vamos lá? Saca só:
Irei adotar alguns pontos aleatórios e substituir no campo vetorial dado lá no enunciado :
Beleza , agora nós precisamos entender como montar o gráfico a partir desses pontos.
Passo 3
Vocês repararam que a gente não consegue substituir nem o e nem o
Po galera, nesse caso em específico, qualquer ponto que a gente escolha vai nos dar exatamente o mesmo vetor!
Esse vetor vai seguir a direção e sentido do campo, sendo em e em .
Mas como vamos montar esses vetores?
Vamos pegar o ponto como exemplo .
Se representarmos esse ponto no plano cartesiano ficará assim:
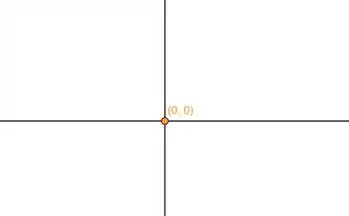
Show. Agora como vimos anteriormente as componentes do vetor serão:
O que isso quer dizer?
Quer dizer que podemos somar/subtrair no ponto de origem os valores :
no eixo
no eixo
Nesse caso, o ponto final será:
Agora vamos dar uma olhada em como ficam esses dois pontos no gráfico:
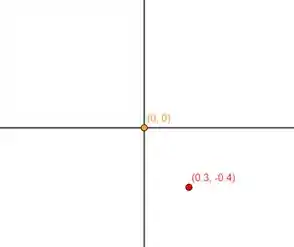
O vetor irá ser a ligação do ponto de origem até o ponto final.
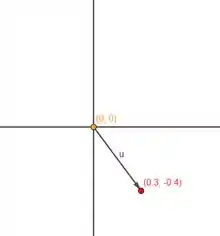
Opa, agora ficou mais claro.
Então podemos afirmar que qualquer ponto vai sempre ter um vetor igual o ali de cima, com mesmo módulo direção e sentido. Beleza?
Um bom esboço disso é:
E tá na mão!
Resposta
