Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 3
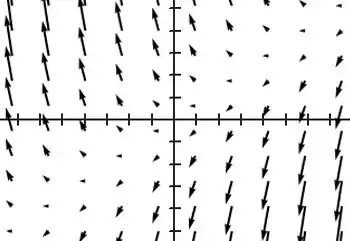
Esboce o campo vetorial desenhando um diagrama como o da Figura 5 ou da Figura 9.
Passo 1
E ai, pessoal!
Nessa questão precisamos esboçar um campo vetorial
Pra isso, vamos analisar essa expressão do campo pra entender como ele muda conforme mudamos o ponto . A gente também vai precisar estudar o tamanho dos vetores, usando a norma deles:
E aí entendendo isso, conseguimos esboçar o campo!
Passo 2
Olhando pro nosso campo
Esse e representam as coordenadas do vetor, então
Daí, já sabemos que todos os vetores do campo têm a primeira coordenada igual a , o que significa que todos estão apontando pro sentido negativo de (esquerda).
Com relação à segunda coordenada, ela vai depender do resultado de .
Vamos ver como essa expressão se comporta no :
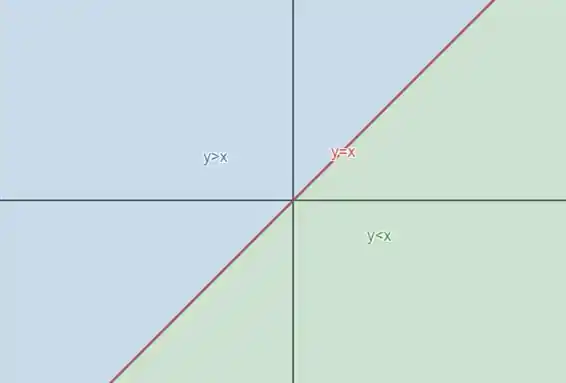
A reta vermelha representa , que é o caso que
Acima dessa reta, na região azul, , então
Já abaixo dela, na região verde, temos e
Tá, mas o que isso quer dizer?
Bom, o sinal dessa expressão é o sinal da segunda componente do vetor, então
- Na reta a segunda coordenada é e o vetor aponta só pra esquerda
- Na região azul, a segunda coordenada é positiva, e o vetor aponta na direção positiva de (pra cima)
- Na região verde, ela é negativa, e o vetor aponta pra baixo.
Passo 3
Calculando a norma do vetor:
Conforme o valor de aumenta, maior é a norma, e, portanto, o tamanho, do vetor.
Isso acontece quando a gente se afasta da reta , já que o começa a ficar muito maior que o , ou vice versa, e assim aumenta.
Com essas informações, já conseguimos desenhar alguns vetores e representar o campo:
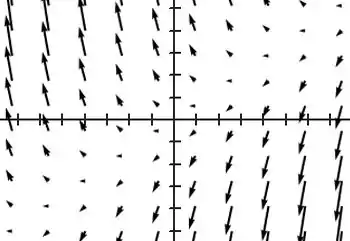
Resposta
