Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 4

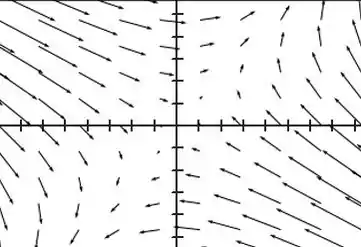
Esboce o campo vetorial desenhando um diagrama como o da Figura 5 ou da Figura 9.

Passo 1

E ai turma, tudo bem? Vamos nessa!

Nossa missão é esboçar o campo vetorial desenhando o diagrama como está na figura ou figura :

Tá, mas como está na figura 5 ou 9? Primeiro devemos entender isso então, como o campo está desenhado.

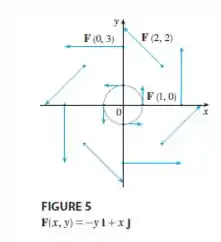
Na figura , o campo tem componentes vetoriais na direção e , logo o vetor pode ter várias direções em relação ao eixo e e ele aumenta conforme se afasta da origem.

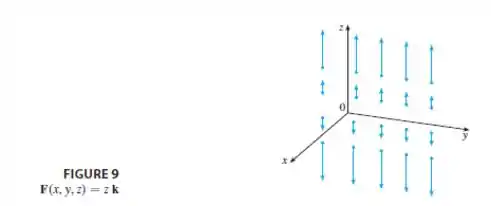
Agora naa figura , que representa um campo no espaço tridimensional. O campo em analise tem apenas componente vetorial na direção , logo ao fazer seu gráfico, vamos ter apenas vetores na direção do eixo que aumentam conforme se afasta da origem.

Com base nisso, nosso objetivo é avaliar quais direções o campo dado no enunciado tem, e se ele tem um tamanho fixo ou pode assumir vários tamanhos. Depois é só fazer um desenho no formato da figura e .

Uma boa estratégia é assumir alguns pontos aleatórios nos quatros quadrantes e encontrar o sentido do vetor associado.

Bora lá!!

Passo 2

Temos o seguinte campo para fazer um esboço:

Você lembra como os quadrantes são divididos né? Caso não lembre, acompanhe a imagem:

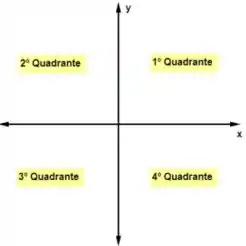
Vamos começar pelo primeiro quadrante com os pontos:

Respectivamente, para cada ponto, temos que nosso campo vetorial se comporta da seguinte forma:

Note que os vetores apontam na direção positiva de x e na direção positiva de y, e crescem conforme se afasta da origem.

Para o segundo quadrante temos os pontos:

Logo, temos que nosso campo vetorial se comporta da seguinte forma:

Note que os vetores apontam na direção positiva de x e na direção positiva de y, e crescem conforme se afasta da origem.

Passo 3

Agora no terceiro quadrante temos os pontos:

Assim, temos que nosso campo vetorial se comporta da seguinte forma:

Note que os vetores apontam na direção negativa de x e na direção negativa de y, e crescem conforme se afasta da origem.

Por fim, o quarto quadrante temos os pontos:

Assim, temos que nosso campo vetorial se comporta da seguinte forma:

Note que os vetores apontam na direção negativa de x e na direção positiva de y, e crescem conforme se afasta da origem.

Notamos que o campo tem um comportamento de afastamento da origem no primeiro e terceiro quadrante, enquanto que no segundo e quarto quadrante os vetores se aproximam da origem.

Com base nisso, podemos ter o seguinte campo vetorial:

Agora pare um pouco!!! Para fixar esse conhecimento, compare os vetores na figura acima, com o que escrevemos antes.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a massa de uma casca esferica de raio R de modo que em todo ponto (x, y, z) sobre a superficie a densidade de massa δ ( x , y , z ) seja sua distancia ate um ponto fixo (a, b, c) da superfici

a) De um exemplo de um campo vetorial F (x, y, z) que tenha valor 0 em apenas um ponto e tal que rot F seja não nulo em todos os pontos. Identifique o ponto e calcule o rotacional.b) De um exemplo de

Encontre todos os pontos (a, b, c) sobre a esfera x 2 + y 2 + z 2 = R 2 onde o campo vetorial F = y z 2 i + x z 2 j + 2 x y z k é normal a superficiee F(a, b, c) ≠ 0.

Esboce um campo de direção para a equação diferencial. Em seguida, use-o para esboçar uma curva de solução que passa por um determinado ponto. y ' = x + y 2 ,( 0 ,0 )

Encontre a integral de linha de ƒ(x, y) = x – y + 3 ao longo dacurva r(t) = (cos t)i + (sen t)j, 0 ≤ t ≤ 2p.