Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 16.Exercícios Adicionais e Avançados - Ex. 05

a) De um exemplo de um campo vetorial F (x, y, z) que tenha valor 0 em apenas um ponto e tal que rot F seja não nulo em todos os pontos. Identifique o ponto e calcule o rotacional.

b) De um exemplo de um campo vetorial F (x, y, z) que tenha valor 0 em precisamente uma reta e de modo que rot F seja não nulo em todos os pontos. Identifique a reta e calcule o

rotacional.

c) De um exemplo de um campo vetorial F (x, y, z) que tenha valor 0 em uma superficie e de modo que rot F seja não nulo em todos os pontos. Identifique a superficie e calcule o rotacional.

Passo 1

Faaaaalaaa meus abençoados, tudo blz?

Na letra (a) temos que criar um exemplo que tanha valor do campo vetorial igual a zero em apenas um ponto e a rotacional seja não numa

Identificando os pontos vamos ter que,

que vai ser igual a 0

Aplicando a rotacional vamos ter que

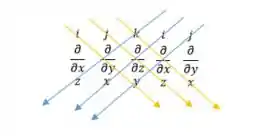
Assim vamos ter que

Passo 2

Já na letra (b) ele também pede um campo vetorial que tenha valor igual a zero em uma reta de moda que a rotacional seja não nula em todos os pontos ,

Identificando um exemplo de reta temos que,

, que é igual a zero apenas na linha

Realizando a rotaciona vamos ter que,

Passo 3

Na letra ( c ) ele pede um exemplo de campo vetorial que seja igual a zero em uma superfície de modo que a rotacional seja não nula em todos os pontos,

Identificando um exemplo temos a função,

, que é igual a zero apenas na linha do plano xy e sua rotacional vai ficar igual,

Resposta

Exercícios de Livros Relacionados

5. Calcular ∫ C f → ⋅ d r → , onde f → = y x 2 + y 2 , - x x 2 + y 2 , ao longo dos seguintes caminhos:d) circungerência de centro na origem e raio 4, no sentido anti-horário.

4. Verificar que as integrais são independentes do caminho de integração e determinar seus valores.g) ∫ 0,0 π , 1 e y c o s xd x + e y s e n xd y

5. Calcular ∫ C f → ⋅ d r → , onde f → = y x 2 + y 2 , - x x 2 + y 2 , ao longo dos seguintes caminhos:a) circunferência de centro em (4,4) e raio 2, no sentido anti-horário;

4. Verificar que as integrais são independentes do caminho de integração e determinar seus valores.e) ∫ 1,1 , 1 1,2 , 3 [ 2 xs e n zd x + z 3 - e y d y + x 2 c o s z + 3 y z 2 d z ]

8. Calcular ∫ C [ x x 2 + y 2 d x + y x 2 + y 2 d y ] , ao longo dos seguintes caminhos:(d) circunferência de centro na origem e raio 1, no sentido anti-horário.