Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 2
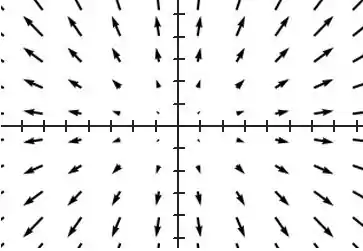
Esboce o campo vetorial desenhando um diagrama como o da Figura 5 ou da Figura 9.
Passo 1
Faala, pessoal!
Nessa questão precisamos esboçar um campo vetorial
Pra isso, vamos analisar essa expressão do campo, pra entender como o campo varia de acordo com o ponto .
Também vamos calcular o tamanho dos vetores do campo, que é dado pela sua norma:
Entendendo como o campo se comporta, vamos desenhar alguns vetores pra representar o diagrama do campo.
Passo 2
O nosso campo é dado por:
Esse e representam as coordenadas do vetor, então:
E a norma é:
Passo 3
Bom, podemos perceber que as coordenadas do vetor em um ponto seguem o mesmo sinal das coordenadas do ponto:
- Se , o vetor aponta pro sentido positivo de
- Se , o vetor aponta pro sentido negativo de
- Se , o vetor é perpendicular ao eixo
E o mesmo vale para . Em resumo:
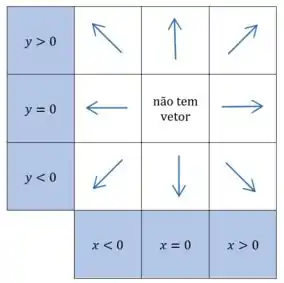
Já a norma do vetor
Conforme o valor de e aumentam, a norma aumenta também. Ou seja, conforme o ponto se afasta de , o que vai fazer e aumentarem, maior é o tamanho do vetor.
Assim, conseguimos desenhar alguns vetores pra representar o campo:
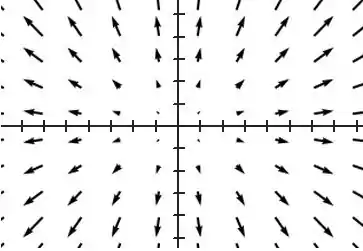
Resposta
