Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 9
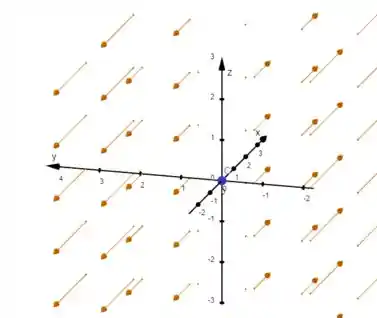
Esboce o campo vetorial desenhando o diagrama como na figura 5 ou figura 9.
Passo 1
Beleza galera, tudo bem? Vamos nessa!!!
Nosso objetivo é esboçar o campo vetorial desenhando o diagrama como na figura ou figura :
Então, vamos primeiro entender como o campo está na figura ou . Veja as figuras abaixo:
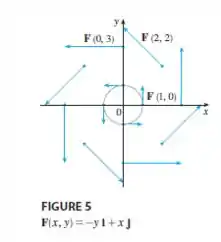
Na figura , repare que o campo tem componentes vetoriais na direção e , logo o vetor pode ter várias direções em relação ao eixo e .
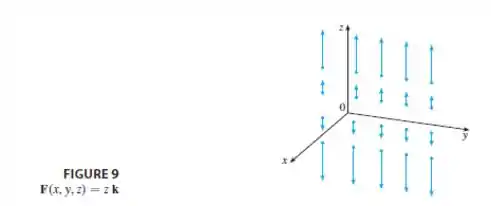
Já na figura , que representa um campo no espaço tridimensional. O campo em analise tem apenas componente vetorial na direção , logo ao fazer seu gráfico, vamos ter apenas vetores na direção do eixo com tamanhos distintos, pois depende do valor de .
Agora, sabendo dessas informações, nosso objetivo é avaliar quais direções o campo dado no enunciado tem, e se ele tem um tamanho fixo ou pode assumir vários tamanhos. Depois é só fazer um desenho no formato da figura e .
Utilize o Geogebra para esboçar o campo vetorial, pois vai facilitar o esboço do gráfico com finitos vetores.
Bora lá resolver!!!
Passo 2
Vamos analisar o vetor fornecido no enunciado:
Repare nesse campo, os vetores possuem comprimento , logo eles estão apontados para a direção positiva do eixo para valores negativos de , e para a direção negativa de para valores positivos de .
Agora podemos pensar um pouco, porque isso acontece? Porque temos uma variável que pode assumir qualquer valor, seja ele positivo ou negativo. E isso gera um campo vetorial com vários tamanhos de vetores.
Logo com o auxílio do Geogebra, podemos ter o seguinte desenho do campo vetorial:
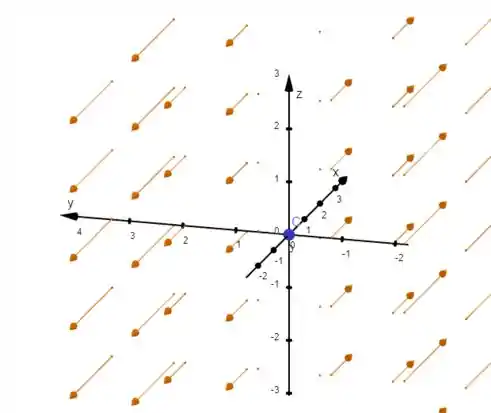
Observe somente a figura, e repare no falamos antes.
Os vetores possuem comprimento , certo? Logo estão apontados para a direção positiva do eixo para valores negativos de e para a direção negativa de para valores positivos de .
Resposta
