Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.10 - Ex. 1

Esboce a curva y = 1 / t e sombreie a região sob a curva cuja área é:

(a) ln ⁡ 2

(b) - ln ⁡ 0,5

(c) 2

Passo 1

Primeiro, esboçando o gráfico de y = 1 t :

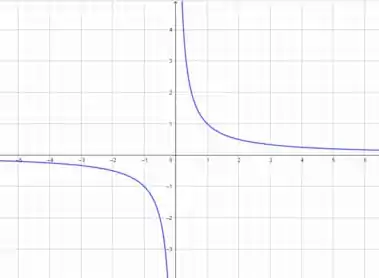
Passo 2

(a) Para achar a área desse gráfico, teríamos que calcular:

∫ 1 t d t = ln ⁡ t + C

Para simplificar nossa vida, sabemos que ln ⁡ 1 = 0 , então se liga:

∫ 1 a 1 t d t = l n ⁡ ( a )

Estamos pegando a área do gráfico a partir de t = 1 , sendo a um número qualquer. Show?

Se queremos que a área seja ln ⁡ 2 , a deve ser igual a 2 , para que:

∫ 1 2 1 t d t = l n ⁡ ( 2 )

Só resolver: ln ⁡ a = ln ⁡ 2 .

Então, vamos colorir a parte do gráfico de t = 1 até t = 2 :

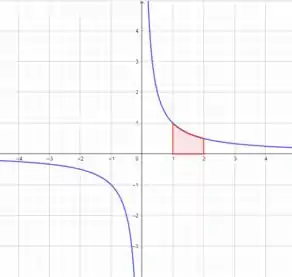
Passo 3

(b) Agora queremos que ln ⁡ a = - ln ⁡ 0,5

Só que:

- ln ⁡ 0,5 = ln ⁡ 0,5 - 1 = ln ⁡ 1 2 - 1 = ln ⁡ 2

Matemágica rs

É o mesmíssimo número do letra (a) kkk vamos apenas repetir:

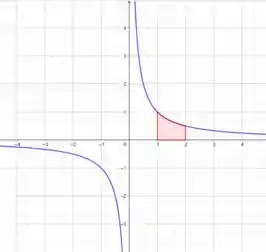
Passo 4

(c) Agora queremos que ln ⁡ a = 2 . Resolvendo isso:

ln ⁡ a = 2

∴

e 2 = a

Pronto, achamos o próximo valor de a . Usando e ≈ 2,72 , e 2 ≈ 7,4 .

Vamos pintar de t = 1 até t = 7,4 :

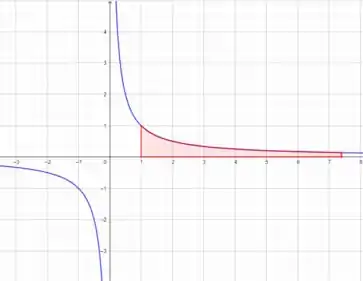
Resposta

(a)

(b)

(c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral: ∫ 4 s e n x + 2 c o s ⁡ ( x ) d x
Calcule a integral: ∫ u 3 - 2 u + 7 d u
Calcule a integral: ∫ x - 2 / 3 - 5 e x d x
Um projétil é disparado verticalmente para cima com uma velocidade inicial de 49m / s , do alto de uma torre com 150m de altura.(a)Quanto tempo irá levar para ele atingir a altura máxima?(b)Qual é a a
1-24. a) Use a Tabela de Integrais para calcular a integral. b) Se o leitor dispuses de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em a).