Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 7
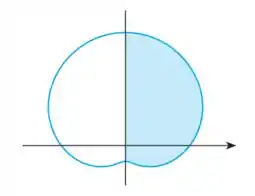
Encontre a área da regiao sombreada, onde .
Passo 1
Opa, tudo tranquilo? Questãozinha de integral em coordenadas polares aqui, vamos lá!
Nosso objetivo é encontrar a área sombreada desse gráfico. Sabemos que a área de uma curva em coordenadas polares é dada pela seguinte fórmula:
Já temos pelo enunciado, só precisamos descobrir qual o intervalo correspondente da região sombreada para completarmos o quebra-cabeça. Quando tivermos todos os dados vamos substituir na integral e encontrar o valor da área.
Passo 2
Mas como a gente encontra esse intervalo? Se a gente sabe que aumenta no sentido anti-horário (de até ) e a nossa região sombreada começa lá no eixo y negativo (onde ) e vai até o eixo y positivo onde ) nós meio que já matamos a charada. Se ficou confuso você pode usar essa imagem abaixo como guia.
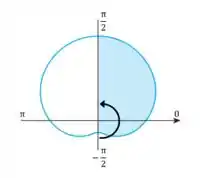
Portanto, o intervalo para a área sombreada será .
Passo 3
Substituindo e o nosso intervalo na fórmula, temos:
Expandindo o termo ao quadrado:
Pelas propriedades de integral, podemos separar em três integrais:
Para a terceira integral, podemos usar a seguinte identidade trigonométrica:
Que nos deixa com a seguinte integral:
Passo 4
Resolvendo a primeira integral:
Resolvendo a segunda integral, lembrando que uma primitiva de seno é :
Resolvendo a terceira, lembrando que uma primitiva de :
Logo, a resposta sera a soma de todas as integrais: