Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 36
Seja a região dentro do laço da curva no Exemplo 1:
- Calcule a área de
- Se girar em torno do eixo encontre o volume do sólido resultante
- Encontre o centroide de
Passo 1
Conforme a letra (a) pede, precisamos achar a área contida no laço do exemplo 1, onde:
Como é um laço, para definirmos os limites de integração usamos pontos que cortem o eixo , ou seja, onde Substituindo percebemos que isso ocorre em .
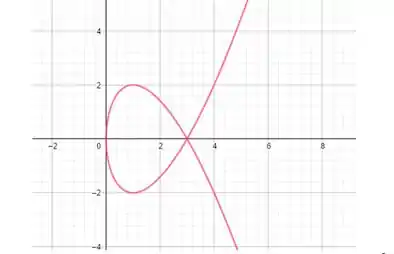
Agora perceba que a curva vem de corta o eixo em , vai até a origem onde e ai fecha o laço em . Então se tomarmos o limite de integração de
e multiplicarmos por temos um meio de chegar no valor da área. Não podemos esquecer que como a curva está negativa nessa parte do laço a área tem que ser multiplicada por .
Passo 2
Depois dessa análise sobre os intervalos chegamos na melhor parte que é integrar. Sabendo que a área será dada por:
É só substituir e diferenciar :
Passo 3
Para a letra (b) pensaremos em cada parte positiva do laço rotacionando o eixo . Sabemos que uma rotação completa de uma circunferência é , e que o raio da nossa rotação seria
Então vamos focar num pequeno retângulo em nosso laço:
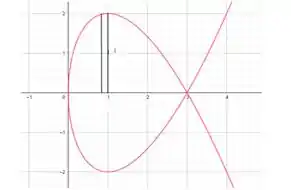
Se esse pequeno retângulo rotacionar perceba que teremos uma área muito próxima de e que se multiplicarmos essa área por teremos o volume de um pequeno disco, da largura de nosso retângulo. Logo o volume do sólido todo formado por essa rotação seria a somatória de todos essas pequenas áreas dos retângulos. Tomando a mesma fórmula da letra (a) vamos continuar considerando aqueles intervalos (não precisamos considerar a área negativa, já que estamos tratando de volume e então elevaremos o raio, , ao quadrado) formando a integral:
Passo 4
Encontraremos agora o centroide de . Para achar o centro de massa fazemos uma média ponderada, por exemplo, para encontrar o centro de massa em fazemos , sendo a área do centro de massa de um retângulo de largura e no fim dividimos tudo pela área totalJá para o centro de massa desse retângulo seria e então as integrais que representam essa somatória e nos indicam o centro de massa:
Nesse nosso retângulo a área será dada por Substituindo então na nossa integral:
Como o laço é simétrico podemos considerar que o em é 0, e então só precisamos encontrar o centro e massa em . Substituindo então pelas equações paramétricas e inserindo os limites de integração de e podemos multiplicar em cima e em baixo por -2
Já sabemos que a integral do denominador é
Multiplicando, tirando o MMC e simplificando chegamos em
Resposta
(a)
(b)
(c)