Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 9
Esboce a curva e calcule a área limitada por ela
Passo 1
Oiii, tudo bem
?? Bom... o enunciado nos deu a seguinte expressão de uma curva (dada em coordenadas polares):
Primeiro vamos esboçar essa curva, depois a gente calcula a área.
Para esboçar, vamos escolher alguns valores de dentro do intervalo e obter os valores de correspondentes. Assim a gente plota os pontos , depois liga.
Já para calcularmos a área vamos aplicar na seguinte integral:
Agora bora lá!! 😉
Passo 2
Primeiramente vamos escolher alguns valores de dentro do intervalo e obter os valores de correspondentes .
Vamos fazer dessa forma manual porque nessa questão ele não pede pra usar ferramenta gráfica, ok?
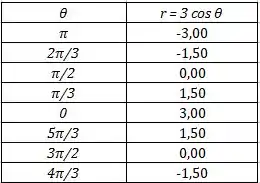
Plotando esses pontos e ligando tudo, vamos ter a curva:
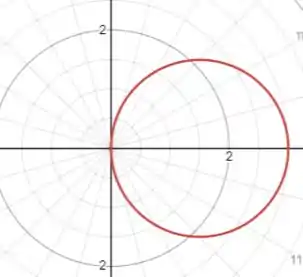
Passo 3
Agora sim vamos calcular a área da curva!
A área de uma curva em coordenadas polares é dada por:
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
O intervalo de integração seria o intervalo em que a curva está definida:
O é a própria parametrização:
Então é só substituir e integrar esse negocio.
Passo 4
Substituindo esses termos, temos:
Abrindo a expressão:
Colocando a constante para fora:
Sabemos que , logo:
Resolvendo as integrais:
Aplicando os limites de integração: