Encontre a área da regiao sombreada, onde .
Passo 1
Em coordenadas polares temos que a área de uma região é dada pela integral onde e a função que determina como o raio da curva varia em relação ao ângulo no intervalo .
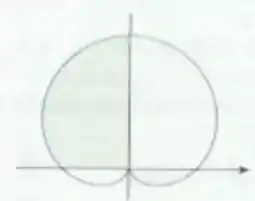
No caso, esta bem explícito qual a função porém, usando a imagem como referência, precisamos descobrir qual o intervalo que será o domínio de integração.
Teremos que
onde é uma primitiva de
Passo 2
Na figura, a área sombreada está no segundo quadrante, então o ângulo percorre, partindo do eixo no sentido anti-horario, partindo do ângulo .
Portanto, partindo do o ângulo percorre , então temos que o intervalo em questão e: .
Passo 3
Como a expressão do raio e dada, já podemos calcular a integral:
Pelas propriedades de integral, podemos separar em três integrais:
A primeira e a segunda são simples, já a terceira precisa de uma substituição:
Usando as relações:
e a fórmula do arco duplo do cosseno:
.
Passando o seno ao quadrado para o outro lado, substituindo e simplificando, temos:
Passo 4
Resolvendo a primeira integral:
Resolvendo a segunda integral, lembrando que uma primitiva de seno é :
Resolvendo a terceira, usando a substituição e lembrando que uma primitiva de :
Passo 5
A resposta será a soma de todas as integrais:
Resposta
a área da regiao sombreada é .