Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 53b
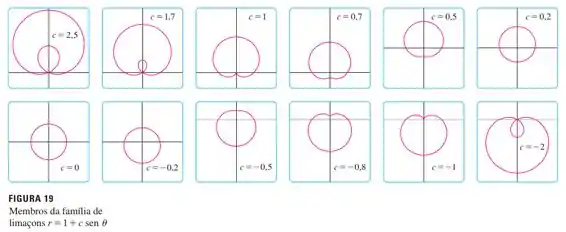
A partir da Figura 19 parece que a limaçon perde sua covinha quando . Demonstre isto.
Passo 1
Olá, meu amigooo. Vou te ajudar a resolver essa querida aqui.
A gente tem a família de limaçons:
E pela figura, quando ele deixa ter convinhas. A gente precisa provar que isso realmente acontece para esse valor.
O que faz a covinha acontecer são os valores de diminuírem ao chegarem próximo do eixo , no ângulo .
Para demonstrar quando isso ocorre, vamos usar o fato de que se a covinha existe
é um ponto de máximo, então a segunda derivada de , que nos diz sobre a concavidadade da função, tem que ser negativa, para termos um ponto de máximo.
Então só precisamos achar para qual valor de a segunda derivada fica positiva, indicando que não tem mais covinha.
Passo 2
Para calcular a segunda derivada de , precisamos primeiro achar primeiramente.
Usando , podemos substituir a equação do limaçon
Fazendo a distributiva
Passo 3
Calculando agora a primeira derivada
E a segunda derivada
Podemos simplificar usando
Em
E para que isso seja negativo
Somando dos dois lados
Dividindo por
Portanto para que a covinha apareça, invertendo a inequação
Resposta
Ver o desenvolvimento.