Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 31
Esboce a curva com a equação dada.
Passo 1
Olá, meu amigo. A gente vai esboçar a curva dada por:
O que a equação representa?
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Para construirmos esse gráfico, poderíamos pegar diferentes ângulos e calcular o para cada um e estimar como seria nosso gráfico.
Outra maneira de construí-lo é mudar para coordenadas cartesianas e então jogar no plano.
Passo 2
Utilizando o segundo método, vamos transformar essa equação em uma equação cartesiana.
Sabemos que , isolando o ficamos com
Substituindo na nossa equação temos que
Multiplicando ambos os lados por ficamos com
Outra relação importante é que , substituindo temos
Passo 3
E essa é uma fórmula de circunferência com o centro deslocado, para descobrirmos o centro, precisaremos completar quadrado nos termos que tem , passando todos os termos para o lado direito
Para completar quadrado precisamos transformar a parte destacada em um produto de soma ou de subtração, mas sem alterar a equação, como temos uma subtração vamos usar o quadrado de uma subtração genérica.
Onde e nós vamos ter que achar.
Para que se torne um quadrado perfeito precisaremos que este quadrado venha com uma constante somando de forma que não altere a equação
Sabemos que , então substituindo temos
Pela igualdade de polinômios, montamos o sistema:
Portanto temos que
Substituindo na nossa equação
Somando dos dois lados
Passo 4
Essa é a fórmula de uma circunferência de raio centrada no ponto .
No plano:
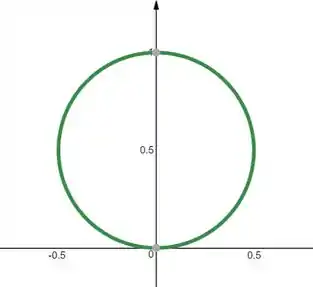
Resposta
