Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 51

Esboce a curva com as equações paramétricas dadas e mostre que ela fica sob um hiperbolóide de uma folha com equação 144 x 2 + 144 y 2 - 25 z 2 = 100 .

x = 27 26 sen ⁡ 8 t - 8 39 sen ⁡ 18 t  

y = - 27 26 cos ⁡ 8 t + 8 39 cos ⁡ 18 t

z = 144 65 sen ⁡ 5 t

Passo 1

Eaee, belezinha?? Bom... o enunciado nos deu as seguintes equações paramétricas:

x = 27 26 sen ⁡ 8 t - 8 39 sen ⁡ 18 t  

y = - 27 26 cos ⁡ 8 t + 8 39 cos ⁡ 18 t

z = 144 65 sen ⁡ 5 t

Queremos esboçar a curva com as equações paramétricas dadas e mostrar que ela fica sob um hiperboloide de uma folha com equação

144 x 2 + 144 y 2 - 25 z 2 = 100

Para isso, podemos pegar as equações paramétricas de x e y e somar o quadrado delas de forma que resulte na equação do hiperboloide dado.

Para esboçar a curva utilizaremos uma ferramenta gráfica.

Passo 2

Fazendo x 2 + y 2 , temos:

x 2 + y 2 = 27 26 sen ⁡ 8 t - 8 39 sen ⁡ 18 t 2 + - 27 26 cos ⁡ 8 t + 8 39 cos ⁡ 18 t 2

Fazendo o produto notável, temos:

= 27 2 26 2 sen 2 ⁡ 8 t - 2 ⋅ 27 ⋅ 8 26 ⋅ 39 cos ⁡ 8 t sen ⁡ 18 t + 8 2 39 2 sen 2 ⁡ 18 t + 27 2 26 2 cos 2 ⁡ 8 t - 2 ⋅ 27 ⋅ 8 26 ⋅ 39 cos ⁡ 8 t cos ⁡ 18 t + 8 2 39 2 cos 2 ⁡ 18 t

Prosseguindo com as multiplicações, temos:

= 27 2 26 2 sen 2 ⁡ 8 t + cos 2 ⁡ 8 t + 64 39 2 sen 2 ⁡ 18 t + cos 2 ⁡ 18 t - 72 169 ( sen ⁡ 8 t sin ⁡ 18 t + cos ⁡ 8 t cos ⁡ 18 t )

Agora, usando as identidades trigonométricas:

sin 2 ⁡ α + cos 2 ⁡ α = 1

e

cos ⁡ x - y = cos ⁡ x cos ⁡ y + sen ⁡ x sen ⁡ y

Podemos simplificar a expressão para:

= 27 2 26 2 + 64 39 2 - 72 169 cos ⁡ ( 18 t - 8 t )

= 27 2 26 2 + 64 39 2 - 72 169 cos ⁡ 10 t

Passo 3

Agora iremos calcular o valor de z 2 :

z 2 = 144 2 65 2 sen 2 ⁡ 5 t

Lançando mão da identidade trigonométrica:

sen 2 ⁡ α = 1 - cos ⁡ α 2

Podemos reescrever a equação para z 2 como:

z 2 = 144 2 65 2 ⋅ 1 2 1 - cos ⁡ 2 ⋅ 5 t = 144 2 2 ⋅ 65 2 - 144 2 2 ⋅ 65 2 cos ⁡ 10 t

Dessa forma, temos que:

144 x 2 + y 2 - 25 z 2 = 144 27 2 26 2 + 64 39 2 - 72 169 cos ⁡ 10 t - 25 144 2 2 ⋅ 65 2 - 144 2 2 ⋅ 65 2 cos ⁡ 10 t

= 144 27 2 26 2 + 64 39 2 - 25.144 2 ⋅ 65 2 - 72 169 cos ⁡ 10 t + 25.144 2 ⋅ 65 2 cos ⁡ 10 t

= 144 27 2 26 2 + 64 39 2 - 72 169 - 72 169 cos ⁡ 10 t + 72 169 cos ⁡ 10 t

= 144 25 26

= 100

Logo, a equação da cruva fica de fato sob o hiperbolóide de uma folha dado no enunciado.

Passo 4

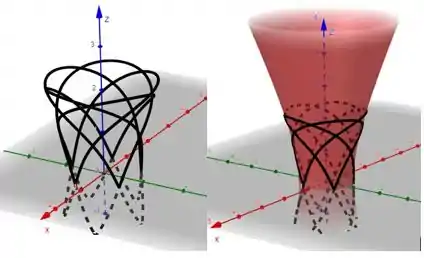
A curva representada por essas equações paramétricas é representada a seguir para o intervalo 0 ≤ t ≤ 2 π .

Para auxiliar na visualização, o gráfico a direita apresenta a superfície fornecida no enunciado, e é possível verificar que a curva está sob a superfície.

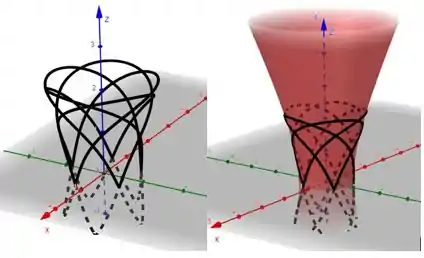
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva. r t =c o s 2 t , c o s 3 t , c o
Trace a curva com equações paramétricas x = s e n t , y = s e n 2 t , z = c o s 4 t . Explique sua forma representando por gráficos suas projeções para os três planos coordenados.
Combine as equações paramétricas com os gráficos (Figuras I-VI). Dê razões para suas escolhas: x = cos ⁡ t , y = sin ⁡ t , z = 1 ( 1 + t 2 )
Combine as equações paramétricas com os gráficos (Figuras I-VI). Dê razões para suas escolhas: x = cos ⁡ 8 t , y = sin ⁡ 8 t , z = e 0,8 t , t ≥ 0
Esboce a curva com a equação vetorial fornecida. Indique uma seta, o sentido na qual t aumenta: r t = t 2 - 1 , t