Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas da grade que têm constante e quais têm constante.
Passo 1
Oi pessoal, vamos analisar essa questão com calma e ver o que ele está pedindo.
Bom , ele quer que a gente plote o gráfico da superfície parametrizada de:
Onde:
e diga quais serão as curvas de grade que têm constante e quais têm constante.
Primeira coisa que vamos fazer é achar os valores correspondentes a e depois plotar o gráfico em um software.
Por último iremos analisar as curvas de grade vendo como as equações ficam com constante e com constante.
Vamos nessa!
Passo 2
Primeiro então vamos achar os valores de . Sabemos que :
Plotando em uma calculadora gráfica 3D, a superfície parametrizada é:
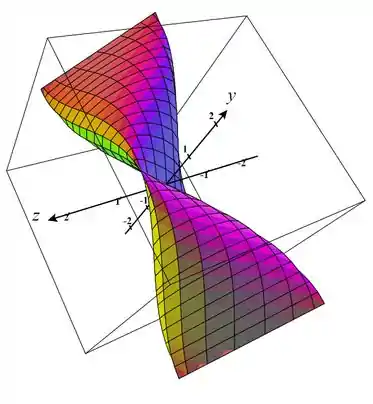
Passo 3
Vamos fazer com que seja constante.
Podemos ver que fica constante e e variam, logo , as curvas correspondentes são curvas paralelas ao plano . 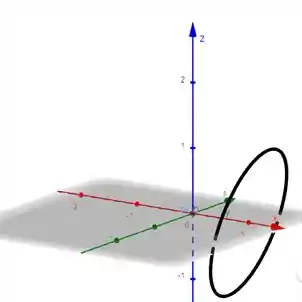
Passo 4
Se fizermos constante,
Logo podemos ver que fica constante e e variam, logo , as curvas correspondentes são curvas paralelas ao plano .
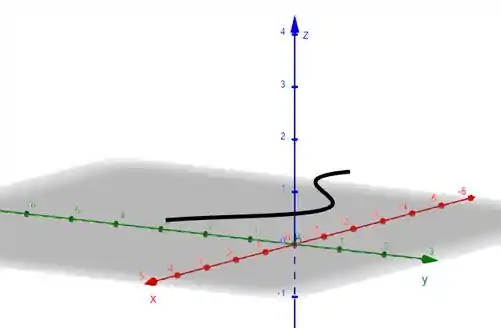
Resposta
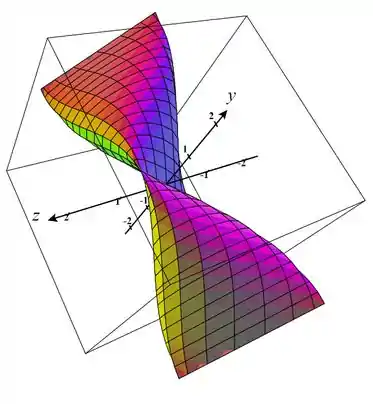
constante as curvas correspondentes são curvas paralelas ao plano .
v constante as curvas correspondentes são curvas paralelas ao plano .