Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 38
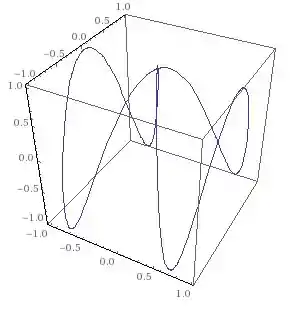
Trace a curva com equações paramétricas , , . Explique sua forma representando por gráficos suas projeções para os três planos coordenados.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu as seguintes equações paramétricas:
Queremos traçar essa curva de forma que a gente faça gráficos e expliquemos suas projeções nos três planos coordenados.
Passo 2
Se liga no que acontece quando fazemos e plotamos o gráfico :
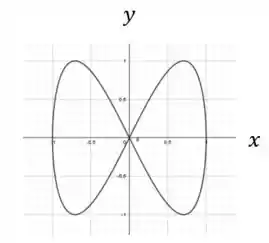
Perceba que o eixo varia “mais rápido” do que o eixo . Isso faz sentido porque o argumento do seno descrito em é maior do que o descrito em .
Além disso, pelo fato de ambas as equações serem de seno, isso justifica a oscilação em torno da origem.
Passo 3
Se liga no que acontece quando fazemos e plotamos o gráfico :
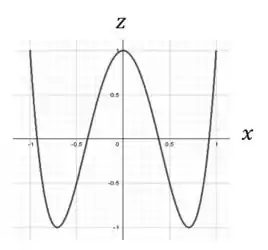
Perceba que o eixo varia “mais rápido” do que o eixo . Isso faz sentido porque o argumento do seno descrito em é maior do que o descrito em .
Além disso, pelo fato de uma equação ser seno e a outra ser cosseno, isso justifica o caráter espelhado em torno da origem.
Passo 4
Por fim, fazendo , podemos observar :
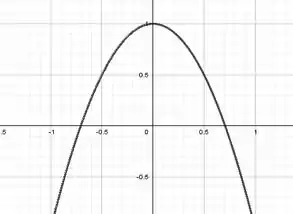
Perceba que o eixo varia “mais rápido” do que o eixo . Isso faz sentido porque o argumento do seno descrito em é maior do que o descrito em .
Além disso, pelo fato de uma equação ser seno e a outra ser cosseno, isso justifica o caráter espelhado em torno da origem.
Passo 5
Assim, plotando no plano , temos:
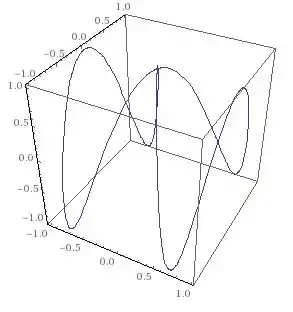
Resposta
