Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 12
Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas da grade que têm constante e quais têm constante.
Passo 1
Beleza,pessoal? Vamos entender o que a questão quer que a gente faça primeiro.
Bom, ela pede para que a gente plote gráfico da superfície parametrizada de:
Onde:
e diga quais serão as curvas de grade que têm constante e quais têm constante.
Vamos começar plotando o gráfico com ajuda de um software com os valores de que ele nos deu.
Depois vamos analisar as curvas de grade vendo como as equações ficam com constante e com constante.
Passo 2
Bom, de acordo com o enunciado :
Plotando em uma calculadora gráfica 3D, a superfície parametrizada é:
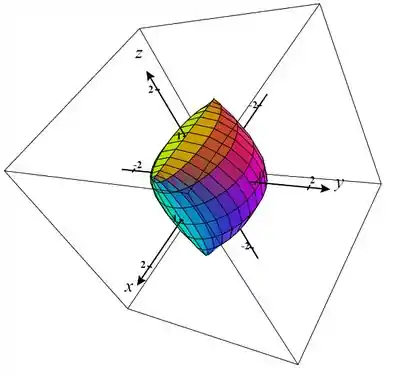
Passo 3
Para descobrir a curva de grade ,bora fazer com que seja constante.
Assim, é constante e as curvas correspondentes são curvas paralelas ao plano .Vamos ver isso graficamente para a gente entender melhor :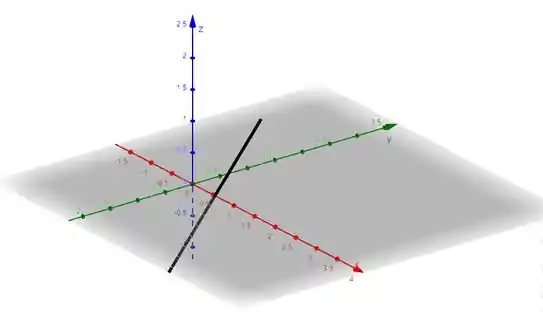 
Passo 4
Se fizermos constante:
Como é constante , as curvas correspondentes são curvas paralelas ao plano .
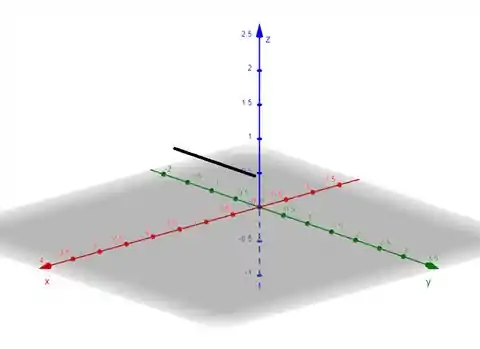
Resposta
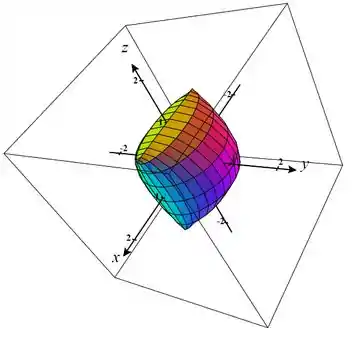
constante as curvas correspondentes são curvas paralelas ao plano
v constante as curvas correspondentes são curvas paralelas ao plano .