Esboce o desenho do sólido descrito pelas desigualdades
Passo 1
Pelas variáveis apresentadas no enunciado temos que o sólido está em coordenadas esféricas. Desta forma podemos verificar como os parâmetros estão variando no plano cartesiano para poder desenhar o gráfico.
Sabemos que , então temos uma “esfera” uma de raio 2
Mas a variação angular ao longo do eixo é , logo temos um ângulo de 60°.
Isso formara uma figura pareceida com um sorvete.
Passo 2
Deste modo o gráfico é:
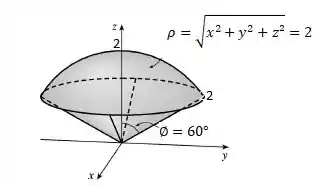
Resposta
Ei, a resposta está no passo a passo :)