Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 17
Esboce o gráfico de cada função e determine se a função tem quaisquer valores extremos absolutos no domínio. Explique a consistência de sua resposta com o Teorema 1.
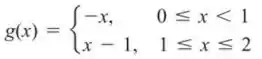
Passo 1
Para verificar se há valores extremos absolutos dessa função dada, podemos aplicar o Teorema 2 e, portanto, aplicar a primeira derivada à função e igualar o resultado a zero. Para este caso, em cada intervalo especificado, a função em questão não possui nenhum ponto crítico (em ambos os intervalos ).
Passo 2
Nesse caso, se torna necessário fazer o desenho da curva da função e obtém-se o seguinte:
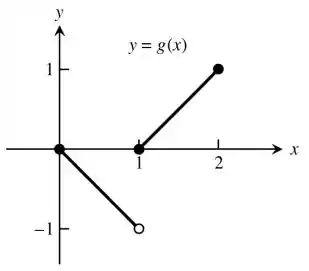
Observando o esboço do gráfico, vemos que existe um máximo absoluto em pelo fato de que o maior valor da função dentro do intervalo de seu domínio é obtido neste ponto. Não há presença de um mínimo local e, consequentemente, não há mínimo absoluto.
Resposta
As condições do Teorema 1 não são atendidas visto que a função possui uma descontinuidade em . No entanto, o fato das condições do Teorema 1 não serem satisfeitas faz com que haja a possibilidade de que existam ou não valores extremos absolutos. Além disso, não se pôde concluir apenas com a primeira derivada se existem ou não mais valores extremos absolutos tornando necessária a análise através do gráfico.