Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 60
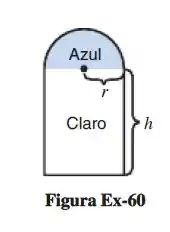
A janela de uma igreja consiste em uma secção semicircular no topo de um retângulo, conforme mostra a Figura Ex-. O vidro azul deixa passar metade da luz por unidade de área. Encontre o raio da janela que admite maior luz se o perímetro de toda a janela for de metros.
Passo 1
Vamos analisar os dados do enunciado, temos que o intervalo é de , e primeiro temos que achar a equação do perímetro, temos três lados de um retângulo e metade de uma circunferência:
Agora vamos achar a expressão da área:
Passo 2
Como queremos encontrar o raio da janela que admite maior luz vamos colocar isolar e substituir em :
Substituindo:
Agora para encontrar o raio da janela que admite maior luz vamos derivar a expressão e igualar a zero para achar o valor máximo, vamos lá!!
Passo 3
Temos então que o ponto crítico é , temos que avaliar o desse ponto junto com os pontos do intervalo :
Vamos calcular o limite no infinito:
Pronto, temos que é um máximo absoluto no intervalo, já que ele possui um valor positivo, e quando tende para o infinito o valor tende a valores negativos, então é o raio da janela que admite maior luz.