Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 6
(a) Esboce o gráfico da curva plana com equação vetorial dada.
(b) Determine r’(t).
(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.
Passo 1
As equações paramétricas correspondentes à função vetorial dada são
Ou
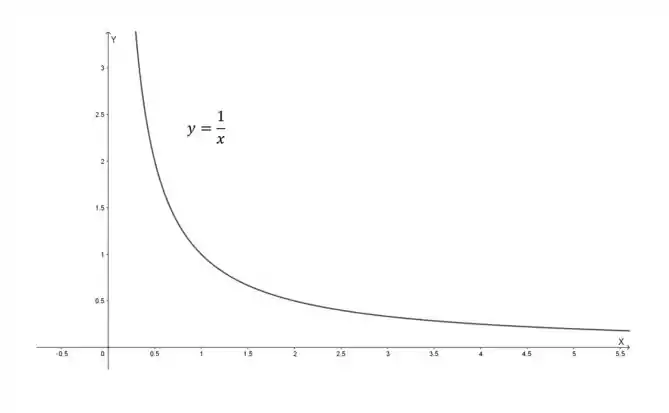
Com base nas equações paramétricas percebemos que
Como a função é positiva para todo , observa-se que e . Portanto o gráfico da curva é dado pelos valores positivos da função .
Passo 2
Determinamos derivando as componentes de .
Passo 3
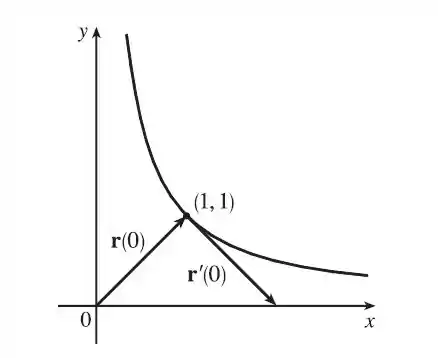
O vetor posição em é
Por outro lado, o vetor tangente em , tem origem no ponto (1,1) e é dado por
Com base nos resultados obtidos podemos representar esses vetores conforme mostrado na figura abaixo:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A temperatura nos pontos de um sólido esférico é dada pelo quadrado da distância do ponto até o centro da esfera. Usando coordenadas cartesianas, determinar o campo temperatura.
Um campo minado tem a forma de um retângulo de lados a e b. O campo foi dividido em pequenos retângulos de lados a m e b n , m e n inteiros e positivos. Os explosivos foram colocados nos vértices dess
Nos exercícios de 1 a 7 representar graficamente os seguintes campos vetoriais.2) f → x , y ,z = x i → + y j → + z k →
Um furacão se desloca na superfície terrestre, atingindo uma faixa retilínea de 20 km de largura. Na zona central da faixa (2 km de largura) a velocidade do vento é de 200 km/h. Nos demais pontos é da
Escrever uma função vetorial em duas dimensões que define um campo vetorial, cuja intensidade seja igual a 1.