Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 7c
- Esboce o gráfico da curva plana com a equação vetorial dada.
- Encontre .
- Esboce o vetor posição e o vetor tangente para o valor dado de .
Passo 1
Fala ai pessoal! Belezinha? Para resolver esta questão basta substituir os dados da equação do vetor tangente e substituir o parâmetro . E depois analisar para projetar o gráfico!
Bora!!!
Passo 2
Galera, a curva é dada pela seguinte equação:
E a derivada da curva é:
O vetor posição em é:
Passo 3
O vetor tangente (derivada) em é:
Passo 4
Vamos entender as componente para formar a curva.
A componente determina a coordenada da curva em função do parâmetro . Para a função dada A amplitude da função é limitada entre e . A função é periódica, repetindo seu padrão ao longo do intervalo
A componente determina a coordenada da curva em função do parâmetro . Para a função dada A amplitude da função também é limitada entre e . Assim como , a função é periódica.
Passo 5
Concluindo...
A curva formada pela função vetorial é uma elipse no plano , onde o ponto se move ao longo da elipse à medida que o parâmetro varia. A amplitude, orientação e tamanho da elipse são controlados pelos coeficientes aplicados às funções seno e cosseno nas componentes e da função vetorial.
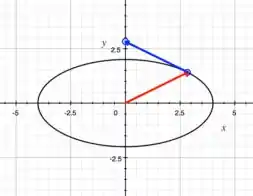
Esboçando o gráfico com os vetores posição e tangente, temos:
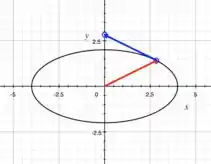
No gráfico acima, o vetor vermelho é o vetor posição e o vetor azul é o vetor tangente.
Resposta
