Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 60c

Sejam vec a e vec b nao-nulos.

(c) Prove: p r o j_vec a vec v = p r o j_vec b vec v <=> vec a ∥ vec b ou ( vec a _|_ vec v e vec b _|_ vec v ) .

Passo 1

Bora lá!

Neste exercício, devemos provar que p r o j_vec a vec v = p r o j_vec b vec v <=> vec a ∥ vec b ou ( vec a _|_ vec v e vec b _|_ vec v ) , beleza?

A melhor maneira de fazermos isso, é através de ilustrações, vamos lá?

Passo 2

Primeiramente, iremos ilustrar a situação na qual vec a ∥ vec b .

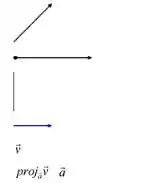
Como podemos notar, quando vec a ∥ vec b , a projeção de vec v sobre os dois vetores será a mesma, pois eles possuem a mesma direção.

Passo 3

Agora, vamos ilustrar o caso em que ( vec a _|_ vec v e vec b _|_ vec v ) .

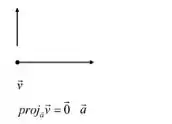
Como podemos notar, quando os vetores vec a e vec b forem ortogonais ao vetor vec v , as projeções serão iguais ao vetor nulo, portanto, iguais.

Assim, provamos o que queríamos 😉.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o vetor a → de módulo 5 , sabendo que é ortogonal ao eixo O y e ao vetor v → = i → - 2 k → , e forma ângulo obtuso com o vetor i → .
Seja o cubo de aresta a representado na Figura 2.17 . Determinar:o ângulo agudo formado por duas diagonais do cubo.
Seja o cubo de aresta a representado na Figura 2.17 . Determinar:o ângulo agudo entre a diagonal do cubo e uma aresta.
Os ângulos diretores de um vetor a → são 45 ° , 60 ° e 120 ° e a → = 2 . Determinar a → .
Determinar o vetor v → nos seguintes casos: v → é ortogonal ao eixo O z , v → = 8 , forma ângulo de 30 ° com o vetor i → e ângulo obtuso com j → .