Use a geometria ou simetria, ou ambas, para calcular a integral dupla.
66.
D é o disco com centro na origem e raio R.
Passo 1
Oi, pessoal, tudo bem?
A questão nos deu uma integral dupla e quer que calculemos ela usando geometria ou simetria, ou dos dois jeitos.
Vamos considerar a expressão:
Melhorando a expressão,
Parece a equação de uma esfera, né? Show!
Com isso temos que , já que a equação original que temos acima é positiva.
Passo 2
Observe que a região é uma esfera centrada na origem e de raio R.
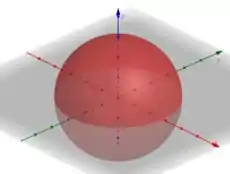
Como estamos trabalhando com uma região onde , nossa região D será positiva.
Iremos utilizar da geometria para encontrar o volume da esfera!
A fórmula para encontrar o volume é:
Como temos um raio e metade positiva para a região, substituindo teremos:
Moleza, né?