Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 17
Esboce o gráfico de um exemplo de função que satisfaça todas as condições dadas.
Passo 1
Eaee, belezinha?? Bom... queremos esboçar um gráfico que satisfaça as seguintes condições:
O enunciado também quer que demos um exemplo de uma função que satisfaça essas condições.
Para isso, perceba que estamos trabalhando com limites laterais. Mas o que são esses limites laterais???
Bom... referem-se aos valores que uma função se aproxima à medida que a variável de entrada se aproxima de um determinado ponto a partir de um lado específico.
Se a função se aproxima de um valor específico à medida que a variável de entrada se aproxima do ponto a partir do lado direito, é chamado de limite lateral direito.
Da mesma forma, se a função se aproxima de um valor específico à medida que a variável de entrada se aproxima do ponto a partir do lado esquerdo, é chamado de limite lateral esquerdo.
Agora vamos aplicar!! ����
Passo 2
Vamos analisar cada uma das condições:
1)
Isso significa que, à medida que se aproxima de pelo lado direito, a função se aproxima de .
2)
Isso indica que, à medida que se aproxima de pelo lado esquerdo, a função se aproxima de
3)
Este limite expressa que, à medida que se aproxima de , a função se aproxima de .
4)
Isso significa que quando é exatamente , o valor de é .
5)
Quando é exatamente , o valor de é .
Passo 3
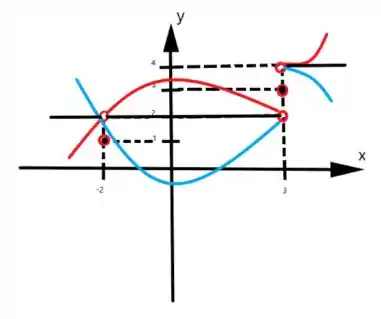
O gráfico a seguir satisfaz todas propriedades pedidas, marcando todos os pontos que o nosso enunciado nos fornece.
Quando x tende a 3 pela direita a função tende a 4 (bolinha aberta);
Quando x tende a 3 pela esquerda a função tende a 2 (bolinha aberta);
Quando x tende a -2, não sabemos se e pela esquerda ou direita, a função tende a 2, como não foi mencionado se o limite e pela esquerda ou direita, indiferente da direção o limite deve ser igual, ela vai sair do ponto (3,2) bolinha aberta para o ponto (-2,2) bolinha aberta.
O gráfico temos duas curvas a concava para baixo, mas nada impede de que seja feita concava para cima.
No gráfico também possui uma reta, que pode ser uma função constante, ela pode satisfazer o que foi pedido.
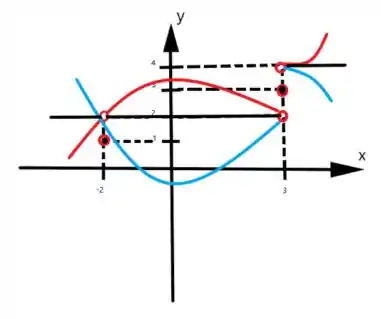
Lembre-se que as bolinhas preenchidas indicam que o ponto pertence a função e as vazias indicam que não pertence.
Resposta
