Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 16
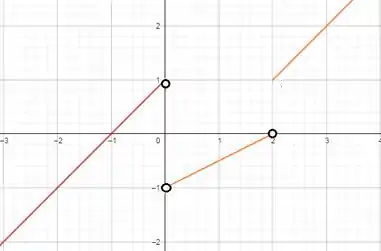
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.
14)
Passo 1
Eaee, belezinha?? Bom... queremos esboçar um gráfico que satisfaça as seguintes condições:
não está definida
O enunciado também quer que demos um exemplo de uma função que satisfaça essas condições.
Para isso, perceba que estamos trabalhando com limites laterais. Mas o que são esses limites laterais???
Bom... referem-se aos valores que uma função se aproxima à medida que a variável de entrada se aproxima de um determinado ponto a partir de um lado específico.
Se a função se aproxima de um valor específico à medida que a variável de entrada se aproxima do ponto a partir do lado direito, é chamado de limite lateral direito.
Da mesma forma, se a função se aproxima de um valor específico à medida que a variável de entrada se aproxima do ponto a partir do lado esquerdo, é chamado de limite lateral esquerdo.
Agora vamos aplicar!! 😉
Passo 2
Muito bem, vamos analisar cada uma das condições que nos foram dadas:
Quando a função se aproxima de pela esquerda, a função tende a ...veja:
E quando se aproxima se pela direita, a função tende a , se liga:
Passo 3
No entanto a função exatamente no ponto não está definida, ou seja, intervalo aberto nele!! Portanto:
não está definida
Agora quando a função se aproxima de pela esquerda, a função tende a :
E quando se aproxima se pela direita, a função tende a :
E no ponto a função vale exatamente , ou seja, intervalo fechado:
Passo 4
Então, uma função que cabe aqui é:
E, plotando o gráfico:
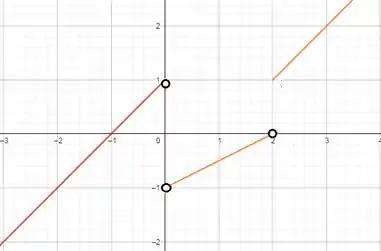
Resposta
