Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 21
Faça uma conjectura sobre o valor do limite (se ele existir) por meio dos valores da função nos números dados (com precisão de seis casas decimais).
Passo 1
Bora entender o que a gente vai fazer aqui!! O problema dá pra a gente esse limite:
E basicamente o que a gente quer é estimar quanto vale essa função quando ela se aproxima de zero.
O problema é que não podemos substituir o zero porque teriamos uma divisão por zero!
Então o que que o enunciado propõe pra a gente?!
A gente vai substituir o por vários valores que se aproximam cada vez mais do zero.
A gente vai fazer isso pela direita e pela esquerda e isso vai mostrar pra a gente qual é o valor desse limite!
Passo 2
Temos:
Os valores que a gente vai substituir são:
O primeiro eu vou fazer junto com você, como é só substituição eu vou deixar a resposta do resto em uma tabelinha pra a gente comparar nossos resultados e ver se ta tudo certinho! Beleza?!
Passo 3
Então vamos começar, para :
O é um número irracional que é aproximadamente igual a , porém como o enunciado pede uma precisão de casas decimais, é melhor usar a função da sua calculadora para calcular!
Agora para
Agora é só fazer o mesmo com os outros valores!!
Construindo uma tabela com os valores de dados e os respectivos ficamos com
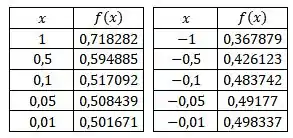
Analisando os dados da tabela, vemos que quando mais se aproxima de zero, mas vai se aproximando de , então podemos dizer que:
Entendeu direitinho?? Responde aee 😉