Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.2 - Ex. 59
Esboce o gráfico da função . Descreva o traçado do gráfico. Por que a função se comporta dessa maneira? Justifique sua resposta.
Passo 1
Primeiramente vamos plotar o gráfico de para, então, podermos explicar sobre esse comportamento.
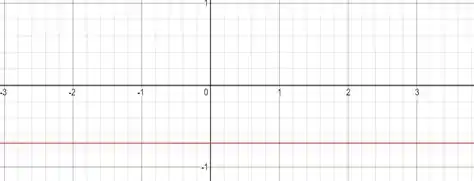
Pela observação do gráfico podemos perceber que ele é uma reta. A estratégia utilizada para mostrar o porquê desse gráfico é tentar encontrar que a derivada é uma constante, haja vista que quando a função original é uma reta.
Passo 2
Derivando através da regra da cadeia obtemos
Lembrando que ) para o caso especial em que temos podemos escrever , substituindo teremos
Como a derivada é constante isso implica a nossa função ser escrita como uma reta , no caso, uma reta de valor constante.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Suponha que f ( 0 )=5 e que f ' ( x )=2 para todo x . Obrigatoriamente, f ( x )=2 x+5 para todox ? Justifique sua resposta.
Mostre que função g t =1 1 - t +1 + t - 3,1 , tem exatamente uma raíz no interior do intervalo (-1,1).
Suponha que f ' x = 2 x para todo x. Determine f ( 2 ) se f 0 = 0 .
Mostre que função f(x) = x 3 + 4 x 2 + 7 , tem exatamente uma raiz no interior do intervalo (- ∞ , 0).
Determine todas as funções possíveis com a derivada y ' =4 x - 1 x .