Mostre que função f(x) = + 7 , tem exatamente uma raiz no interior do intervalo (-, 0).

Analisando a função e testando alguns valores inteiros para tentar achar as raízes conseguimos verificar que -2 é raiz, da seguinte forma:

Pegando 2 valores próximos de -2 como -2,1 e -1,9 e aplicando na função vemos que . Sendo assim, pelo teorema do valor intermediário percebemos que existe uma raiz nesse intervalo e que já descobrimos no passo anterior que é o -2. Analisando graficamente a função observamos o seguinte:

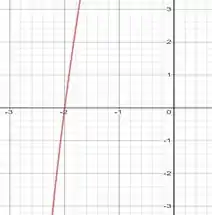
se e que se . Sendo assim, garantimos que a função tem exatamente uma raiz apenas no intervalo dado.