Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 29
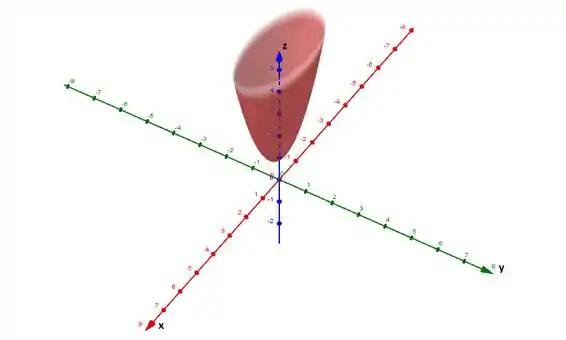
Esboce o gráfico da função.
Passo 1
Olá, caro estudante. Vamos resolver mais uma atividade?
Queremos determinar o gráfico da função:
Para esboçarmos o gráfico de uma função de duas varáveis precisamos primeiramente encontrar as curvas de nível desta função.
Para isso façamos:
A partir disso, iremos analisar alguns pontos dessa função. Iremos analisar o seu comportamento para diferentes valores de , isso nos dará a noção de como é o formato da curva de nível e consequentemente nos dirá como é o formato da nossa figura.
Também analisaremos os pontos de intersecção da nossa figura com os eixos ordenados. Para isso, deveremos zerar duas variáveis, e teremos então o valor da intersecção da variável que sobrá.
Passo 2
Se analisarmos o domínio dessa função, veremos que nunca pode ser menor que , pois se isso acontecer teremos um resultado negativo e dois números ao quadrado no conjunto dos reais nunca é negativo.
Então tendo em mente essa restrição vamos escolher alguns valores para :
, e .
Desta forma obtemos as seguintes curvas de nível:
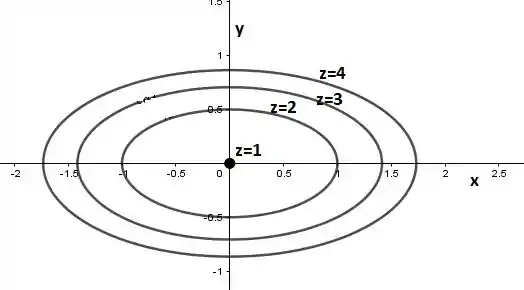
Iremos encontrar as intersecções da curva com os eixos.
Para
Veja que aqui temos uma afirmação falsa, não podemos ter dois números quadrados resultando em um número negativo, isso nos diz que não existe intersecção com esse eixo, e também não teremos, por motivo similar, com o eixo , então a nossa figura irá crescer no sentido positivo de , a partir de
Passo 3
Desta forma o gráfico de é:
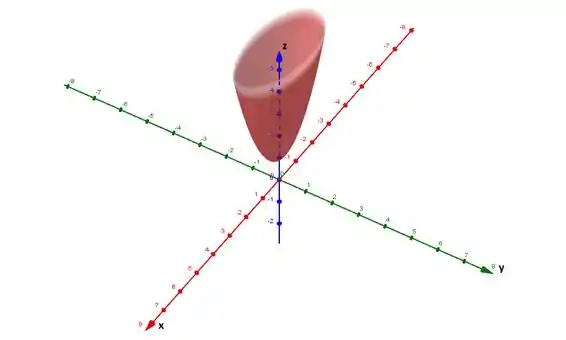
Resposta
