Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.7 - Ex. 20

Esboce o gráfico de uma função g para a qual

g 0 = g ' 0 = 0   ,     g ' - 1 = - 1   ,   g ' 1 = 3   e   g ' 2 = 1  

Passo 1

Olá, meu amigo. Vou te ajudar a resolver essa atividade.

Aqui a gente precisa esboçar o gráfico de uma função que atenda aos requisitos dados:

g 0 = g ' 0 = 0   ,     g ' - 1 = - 1   ,   g ' 1 = 3   e   g ' 2 = 1  

Por conta de g 0 = g ' 0 = 0 nós sabemos que o gráfico tem o ponto ( 0,0 ) e que este pode ser um mínimo local, máximo local ou ponto de inflexão.

Por conta de g ' - 1 = - 1 < 0 nós sabemos que x = - 1 e o gráfico está diminuindo, e por conta de g ' 1 = 3 > 0 nós sabemos que o gráfico está crescendo em x = 1 .

Também temos a informação que g ' 2 = 1 > 0 , isso significa que o gráfico também está aumentando, mas o gráfico é mais inclinado em   x   =   1   do que em   x   =   2   .

Então é com essas observações que iremos criar o esboço desse gráfico.

Passo 2

Para esboçar essa curva e usando as informações que sabemos, podemos afirmar o seguinte:

  1. A curva corta a origem, pois g 0 = g ' 0 = 0  
  2. O ponto ( 0,0 ) é um ponto de mínimo, pois   g ' - 1 = - 1 , ou seja, em x = - 1   a curva é decrescente e g ' 1 = 3 , ou seja, em x = 1 a curva é crescente, então, podemos concluir que ( 0,0 ) é um ponto de mínimo da função
  3. Como g ' 1 = 3   e   g ' 2 = 1 , podemos concluir que a inclinação da reta tangente vai diminuindo, ou seja, a função está ficando “menos íngreme”

De acordo com tudo que pudemos afirmar, esboçaremos agora o gráfico da função g

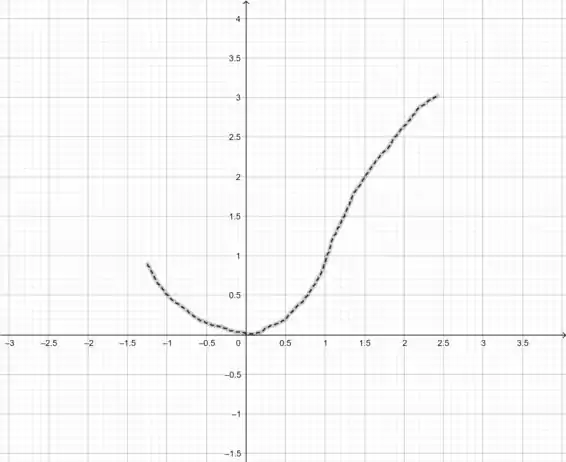
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine todos os pontos da curva y = c o t g x , para 0xπ , em que a tangente é paralela à reta y = - x . Esboce a curva e a(s) tangente(s) no mesmo gráfico, identificando cada uma com sua equação.
Determine todos os pontos da curva y = t g x , para - π / 2xπ / 2 , em que a tangente é paralela à reta y = 2 x . Esboce a curva e a(s) tangente(s) no mesmo gráfico, identificando cada uma com sua equ
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.18)y = 2 x - x 3 ; ( - 2,4 )
Nos exercícios de 1 a 6, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m no intervalo fechado [ a , b ] e inclua na tabela os pontos onde
Nos exercícios de 1 a 6, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m no intervalo fechado [ a , b ] e inclua na tabela os pontos onde