Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 69
Esboce o gráfico de uma função contínua tal que:
- para quando quando .
- para quando para x >2 e quando .
Passo 1
Item a:
Queremos um gráfico com o ponto (2,2), tal que a derivada seja positiva para x
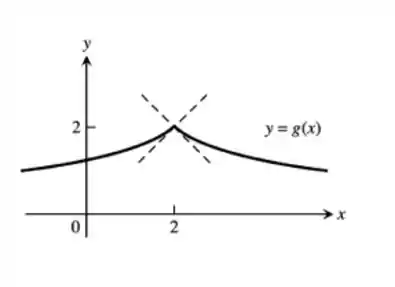
Passo 2
Item b:
Agora queremos um gráfico com derivada negativa onde x 2. Observe que temos o mesmo ponto, e o gráfico será igual ao anterior, porém com períodos de crescimento trocados:
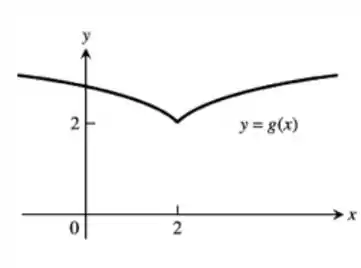
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
O gráfico de f ' está mostrado na figura. Esboce o gráfico de f se f for contínua e f 0 = - 1 .
Suponha que f 3 = 2 , f ' 3 = 1 2 e f ' x0 e f ' ' x0 para todo x .(a) Esboce um gráfico possível de f .(b) Quantas soluções a equação f x = 0 tem? Por quê?(c) É possível que f ' 2 = 1 3 ? Por quê?
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf