Esboce o gráfico de uma função contínua y = h ( x ) tal que: h 0 = 0 , - 2 ≤ h x ≤ 2 para todo x ,h ' x → ∞ quando x → 0 - , eh x → ∞ quando x → 0 + . h 0 = 0 , - 2 ≤ h x ≤ 0 para todo x ,h ' x → ∞ quando x → 0 - , eh x → - ∞ quando x → 0 + .

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 70

Esboce o gráfico de uma função contínua tal que:

para todo x quando quando .

para todo x quando quando .

Passo 1

Item a:

Queremos um gráfico que passe pelo ponto (0,0) , que esteja compreendido em (a função não passa desses valores verticalmente). Além disso, a derivada tende ao infinito antes e depois de zero (logo, a função vai ser sempre crescente fora do ponto x = 0 )

Temos o gráfico:

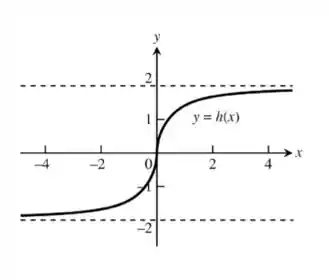
Passo 2

Item b:

Queremos um gráfico que passe pelo ponto (0,0) , que esteja compreendido em (a função não passa desses valores verticalmente). Além disso, a derivada tende ao infinito antes de zero e a menos infinito depois de zero (logo, a função vai ser crescente antes de x = 0 e decrescente depois de x = 0)

Temos o gráfico:

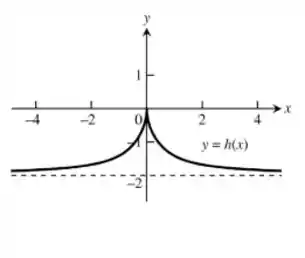
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf

(a) Encontre as assíntotas vertical e horizontal.(b) Encontre os intervalos nos quais a função é crescente ou decrescente.(c) Encontre os valores máximos e mínimos locais.(d) Encontre os intervalos de