Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 67
Esboce o gráfico de uma função derivável que passe pelo ponto (1,1) se
e:
-
para x
f ' ( x ) < 0 para x > 1; -
para x
f ' x > 0 para x>1 - para
- para
Passo 1
Procuramos gráficos que passem no ponto (1,1) e que possuem ponto crítico em x=1, ou seja um ponto de máximo ou mínimo.
O que vai determinar o tipo de extremo será o sinal da derivada de cada item.
Passo 2
-
para x
f ' ( x ) < 0 para x > 1;
Aqui queremos um gráfico que possua um máximo relativo em x=1:
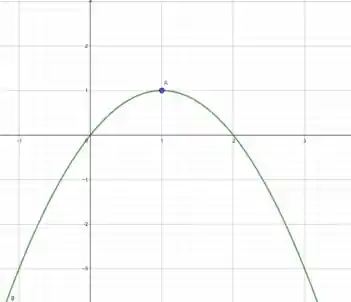
Passo 3
para x
Aqui queremos um gráfico com ponto mínimo relativo em x=1:
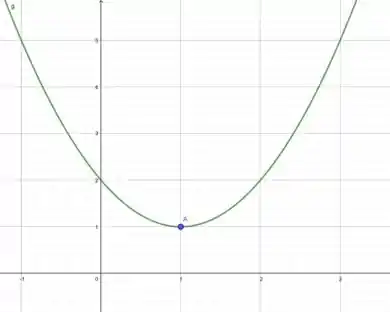
Passo 4
para
Aqui queremos uma função que seja crescente em todo o ponto, menos em x=1:
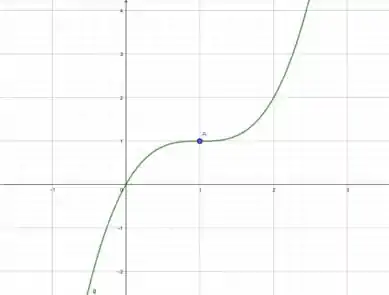
Passo 5
para
E agora queremos uma função que seja decrescente em todos os pontos, menos em x=1:
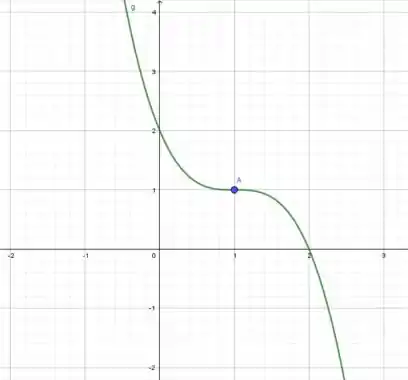
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial. e arctg x = x 3 + 1
Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial. 3 sen x 2 = 2 x
Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial. 4 e - x 2 sen x = x 2 - x + 1
Use o método de Newton com x 1 = 1 para encontrar a raiz da equação x 3 - x = 1 com precisão de seis casas decimais.Resolva a equação da parte (a) usando como aproximação inicial x 1 = 0,6 .Resolva a
Use o roteiro desta seção para esboçar a curva. y = e s e nx